题目内容
如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求△ABC所扫过的图形的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.

解:(1)连接BF,由题意知△ABC≌△EFA,BA∥EF,且BA=EF
∴四边形ABFE为平行四边形,
∴S平行四边形ABFE=2S△EAF
∴△ABC扫过图形的面积为S平行四边形ABFE+S△ABC=2×3+3=9;
(2)由(1)知四边形ABFE为平行四边形,且AB=AE,
∴四边形ABFE为菱形,
∴AF与BE互相垂直且平分.
(3)过点B作BD⊥CA于点D,
∵AB=AE,
∴∠AEB=∠ABE=15°.
∴∠BAD=30°,BD= AB=
AB= AC.
AC.
∴ BD•AC=3,
BD•AC=3,
∴ AC•AC=3.
AC•AC=3.
∴AC2= 12.
12.
∴AC=2 .
.


练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 ,求sinC的值.
,求sinC的值.


 B.
B. C.
C.
 D.
D. 
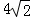 ,求点G到BE的距离.
,求点G到BE的距离.
 AB,设△ABC的外心为O.
AB,设△ABC的外心为O.