题目内容
(如图,在△ABC中,BC=AC,且CD∥ AB,设△ABC的外心为O.
AB,设△ABC的外心为O.
(1)用尺规作出△ABC的外接圆O.(不写作法,保留痕迹)
(2)在(1)中,连接OC,并证明OC是AB的中垂线;
(3)直线CD与⊙O有何位置关系,试证明你的结论.

解:(1)如图所示:
(2)方法一:
连接BO、CO、OA,
∵OB=OA,AC=BC,
∴OC是AB的中垂线;
方法二:
在⊙O中,∵AC=BC,
∴ =
= ,
,
∴∠BOC=∠AOC,
∵OB=OA,
∴OC是AB的中垂线;
(3)直线CD与⊙O相切,
证明:∵CD∥AB,CO是AB的垂线,
∴∠OCG=90°,
∴直线CD与⊙O相切.


练习册系列答案
相关题目

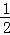 EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠ACD=120°,则∠MAB的度数为 .
EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠ACD=120°,则∠MAB的度数为 .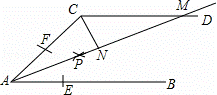

 ,则a>0;
,则a>0;