题目内容
20.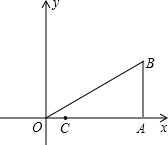 在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=3,以O为原点,OA所在的直线为x轴,建立如图所示的直角坐标系,点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,当PA+PC取最小值时.
在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=3,以O为原点,OA所在的直线为x轴,建立如图所示的直角坐标系,点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,当PA+PC取最小值时.(1)在图中确定点P的位置,并保留作图痕迹(不要求尺规作图);
(2)求出PA+PC的最小值.
分析 (1)根据对称轴上的点到线段两端点的距离相等,可得D点,根据两点之间线段最短,可得答案;
(2)根据直角三角形的性质,可得DE、OE的长,根据勾股定理,可得答案.
解答 解:如图: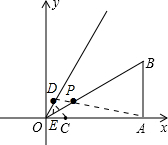 ,
,
(2)DC关于OB对称,作DE⊥OA于E点,得
OD=OC=$\frac{1}{2}$,∠DOC=60°,
△ODC是等边三角形.
DE=$\frac{\sqrt{3}}{4}$,OE=$\frac{1}{4}$.
AE=3-$\frac{1}{4}$=$\frac{11}{4}$.
由勾股定理,得
AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=$\sqrt{(\frac{11}{4})^{2}+(\frac{\sqrt{3}}{4})^{2}}$=$\frac{\sqrt{31}}{2}$.
PA+PC=PA+PD=AD=$\frac{\sqrt{31}}{2}$.
点评 本题考查了轴对称,利用了轴对称的性质,线段的性质,勾股定理,利用轴对称得出等边三角形的判定是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )
由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )
 由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )
由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )| A. | 4种 | B. | 3种 | C. | 2种 | D. | 1种 |
9.为了了解我市15000名学生的视力情况,抽查了解1000名学生的视力进行统计分析,下列四个判断正确的是( )
| A. | 15000名学生是总体 | |
| B. | 样本容量是1000名 | |
| C. | 每名学生是总体的一个样本 | |
| D. | 1000名学生的视力是总体的一个样本 |


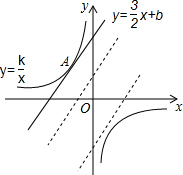 如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.
如图,已知双曲线y=$\frac{k}{x}$与直线y=$\frac{3}{2}$x+b.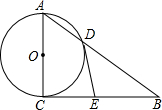 如图,以Rt△ABC的直角边AC为直径的圆⊙O交斜边AB于点O,过D作⊙O的切线DE,交CB于E.
如图,以Rt△ABC的直角边AC为直径的圆⊙O交斜边AB于点O,过D作⊙O的切线DE,交CB于E.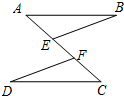 如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.
如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.