题目内容
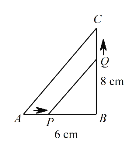
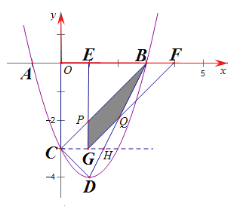
【题目】如图1,已知抛物线C1:![]() 与x轴的一个交点为A(-1,0),另一个交点为B,与
与x轴的一个交点为A(-1,0),另一个交点为B,与![]() 轴的交点为C(0,-3),其顶点为D.
轴的交点为C(0,-3),其顶点为D.
(1)求抛物线C1的解析式;
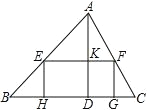
(2)如图1,将△OBC沿![]() 轴向右平移m个单位长度(0﹤
轴向右平移m个单位长度(0﹤![]() ≤
≤![]() )得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
)得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
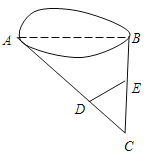
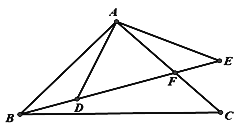
(3)如图2,将抛物线C1平移,使其顶点为原点O,得到抛物线C2.若直线![]() 与抛物线C2交于S、T两点,点
与抛物线C2交于S、T两点,点![]() 是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.
是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.


【答案】(1)![]() ;(2)S=
;(2)S=![]() ;(3)存在一点R,点R关于点
;(3)存在一点R,点R关于点![]() 的中心对称点K也在抛物线
的中心对称点K也在抛物线![]() 上.
上.
【解析】
(1)将已知的抛物线上两点的坐标代入抛物线中进行求解即可.
(2)、(3)见详解.
解:(1)∵ ![]() ,
,![]() 在抛物线
在抛物线![]() 上
上
∴ ![]() 解得
解得 ![]()
∴抛物线![]() 的解析式为
的解析式为![]()
(2)设直线![]() 的解析式为
的解析式为![]() ,
,
则 ![]() 解得
解得![]()
∴ 直线![]() 的解析式为
的解析式为![]() .
.
△![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位长度(0﹤
个单位长度(0﹤![]() ≤
≤![]() )得到△
)得到△![]()
易得直线![]() 的解析式为
的解析式为![]()
设直线![]() 的解析式为
的解析式为![]()
则![]() 解得
解得![]()
则直线![]() 的解析式为
的解析式为![]()
如图![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,![]()
联立![]() 解得
解得![]()
即点![]() (
(![]() ,
,![]() )
)
∴ ![]()
=![]()
![]()
(3)设![]() (
(![]() ,4),若抛物线
,4),若抛物线![]() :
:![]() 上存在一点
上存在一点![]() (
(![]() ,
,![]() ),
),
则点![]() 关于点
关于点![]() 成中心对称的点为K(
成中心对称的点为K(![]() ,
,![]() )
)
假设![]() (
(![]() ,
,![]() )在抛物线
)在抛物线![]() :
:![]() 上
上
∴ ![]()
整理得关于 ![]() 的一元二次方程
的一元二次方程 ![]()
![]()
![]()
∵ 点![]() (
(![]() ,4)在线段
,4)在线段![]() 上且不与
上且不与![]() 、
、![]() 重合
重合
∴ ![]() 则
则 ![]()
∴ ![]()
故关于![]() 的一元二次方程有两个不相等的实数根.
的一元二次方程有两个不相等的实数根.
∴抛物线![]() 上存在一点R,点R关于点
上存在一点R,点R关于点![]() 的中心对称点K也在抛物线
的中心对称点K也在抛物线![]() 上.
上.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目