题目内容
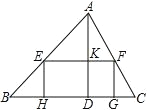
【题目】如图，锐角△ABC 中，BC＝12，BC 边上的高 AD＝8，矩形 EFGH 的边 GH在 BC 上，其余两点 E、F 分别在 AB、AC 上，且 EF 交 AD 于点 K
(1) 求
的值
(2) 设 EH＝x，矩形 EFGH 的面积为 S
① 求 S 与 x 的函数关系式
② 请直接写出 S 的最大值
【答案】（1）
；（2）①S=
；②24.
【解析】
（1）根据EF∥BC，可得∵ 
∥
∴ △
∽△
∴ 
，据此求出
的值是多少即可．
（2）①首先根据EH=x，求出AK=8-x，再根据
，求出EF的值；然后根据矩形的面积公式，求出S与x的函数关系式，②利用配方法，求出S的最大值是多少即可．
解：（1）∵ 四边形
是矩形
∴ ∥
∵ 
∴ 
∵ ∥
∴ △∽△
∴
（2）∵四边形是矩形
∴ 
°
∵
∴ 
°
∴ 四边形
是矩形
∴ 
∵ 
∴ 
∵
∴ 
∴ 
（3）24
练习册系列答案
相关题目
