题目内容
10.若关于x的方程$\frac{2kx+m}{3}$=2+$\frac{x-nk}{6}$无论k为何值时.它的解总是x=1,求m、n的值.分析 把x=1代入方程,整理后根据无论k为何值时.它的解总是x=1,求出m与n的值即可.
解答 解:把x=1代入方程得:$\frac{2k+m}{3}$=2+$\frac{1-nk}{6}$,
去分母得:4k+2m=12+1-nk,即(n+4)k+2m-13=0,
由无论k为何值时.它的解总是x=1,得到n+4=0,即n=-4,2m-13=0,即m=$\frac{13}{2}$,
则m=$\frac{13}{2}$,n=-4.
点评 此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.解方程$\frac{5}{9}$($\frac{9}{5}$x+1)=1,下列变形最简单的是( )
| A. | 方程两边同时乘以9,得5($\frac{9}{5}$x+1)=9 | B. | 方程两边同时乘$\frac{9}{5}$,得$\frac{9}{5}$x+1=$\frac{9}{5}$ | ||
| C. | 去括号,得x+$\frac{5}{9}$=1 | D. | 括号内先通分,得$\frac{5}{9}$×$\frac{9x+5}{5}$=1 |
18.把代数式ax2-4ax+4a分解因式,下列结果中正确的是( )
| A. | a(x-2)2 | B. | a(x+2)2 | C. | a(x-4)2 | D. | a(x-2)(x+2) |
5.计算(2.5×103)3×(-0.8×102)2的结果是( )
| A. | 6×1013 | B. | -6×1013 | C. | 2×1013 | D. | 1014 |
 如图,公园里设计了曲折迂回的九曲桥,与修一座笔直的桥相比,这样做是否增加了游人在桥上行走的路程?说出其中的道理.
如图,公园里设计了曲折迂回的九曲桥,与修一座笔直的桥相比,这样做是否增加了游人在桥上行走的路程?说出其中的道理. 如图,下列各式能够表示图中阴影部分的面积的是( )
如图,下列各式能够表示图中阴影部分的面积的是( )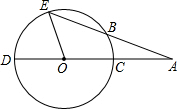 CD是⊙O的直径,AE交⊙O于点B,且AB=OC,∠A=25°,求∠EOD的度数.
CD是⊙O的直径,AE交⊙O于点B,且AB=OC,∠A=25°,求∠EOD的度数.