题目内容
6.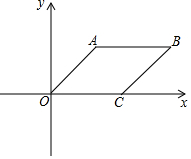 如图,四边形OABC是菱形,点A(3,4),点C在x轴正半轴上,求:直线BC的表达式.
如图,四边形OABC是菱形,点A(3,4),点C在x轴正半轴上,求:直线BC的表达式.
分析 由A点坐标求出AO,利用菱形的性质得出点B和点C的坐标,设直线BC的解析式是y=kx+b,把B、C两点坐标代入得到方程组,解方程组即可得到直线BC的表达式.
解答 解:∵A(3,4),
∴AO=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形OABC是菱形,
∴OC=AB=AO=5,AB∥OC,
∴B(8,4),C(5,0).
设直线BC的解析式是y=kx+b,
把B(8,4),C(5,0)代入得:
$\left\{\begin{array}{l}{8k+b=4}\\{5k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{20}{3}}\end{array}\right.$,
∴直线BC的解析式为 y=$\frac{4}{3}$x-$\frac{20}{3}$.
点评 本题考查了待定系数法求一次函数解析式,菱形的性质,正确求出点B和点C的坐标是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
11.一元二次方程x2-6x-10=0配方后可变形为( )
| A. | (x-3)2=19 | B. | (x-3)2=1 | C. | (x+3)2=19 | D. | (x+3)2=1 |
18.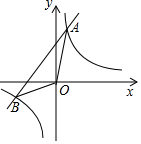 如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
(1)填表:
(2)当k=n(n为正整数)时,试求直线AB的解析式(用含n的式子表示);
(3)当k=1、2、3、…n时,△ABO的面积,依次记为S1、S2、S3…Sn,当Sn=40时,求双曲线y=$\frac{k+1}{x}$的解析式.
 如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根
如图,点A、B是双曲线y=$\frac{k+1}{x}$(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx-k-1=0的两根(1)填表:
| K | 1 | 2 | 3 | … | n(n为正整数) |
| A点的横坐标 | 1 | 1 | 1 | … | 1 |
| B点的横坐标 | -2 | -3 | -4 | … | -n-1 |
(3)当k=1、2、3、…n时,△ABO的面积,依次记为S1、S2、S3…Sn,当Sn=40时,求双曲线y=$\frac{k+1}{x}$的解析式.
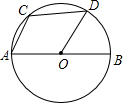 如图,已知AB是⊙O的直径,弦AC与半径OD平行.
如图,已知AB是⊙O的直径,弦AC与半径OD平行.