题目内容
等边△ABC内接于⊙O,AB=10cm,则⊙O的半径是
cm.
| 10 |
| 3 |
| 3 |
| 10 |
| 3 |
| 3 |
分析:作直径AD,连接BD,根据等边三角形性质求出∠C=60°,根据圆周角定理求出∠D=∠C=60°,解直角三角形求出AD即可.
解答:
解:如图,作直径AD,连接BD,
∵等边△ABC内接于⊙O,AD为直径,
∴∠C=60°=∠D,∠ABD=90°,
∵sinD=
,
∴AD=
=
=
cm,
∴⊙0的半径是
cm,
故答案为:
.

解:如图,作直径AD,连接BD,
∵等边△ABC内接于⊙O,AD为直径,
∴∠C=60°=∠D,∠ABD=90°,
∵sinD=
| AB |
| AD |
∴AD=
| AB |
| sin60° |
| 10cm | ||||
|
20
| ||
| 3 |
∴⊙0的半径是
| 10 |
| 3 |
| 3 |
故答案为:
| 10 |
| 3 |
| 3 |
点评:本题考查了等边三角形的性质,圆周角定理,解直角三角形的应用,关键是能正确作出辅助线.

练习册系列答案
相关题目
 已知等边△ABC内接于⊙O,点D是⊙O上任意一点,则sin∠ADB的值为( )
已知等边△ABC内接于⊙O,点D是⊙O上任意一点,则sin∠ADB的值为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|

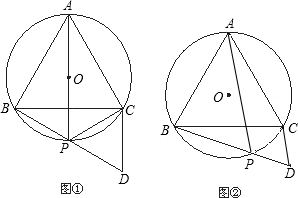 明理由;
明理由; 7、如图,等边△ABC内接于⊙O,以O为旋转中心,能使旋转后的图形与原图形重合.下列符合条件的旋转角是( )
7、如图,等边△ABC内接于⊙O,以O为旋转中心,能使旋转后的图形与原图形重合.下列符合条件的旋转角是( )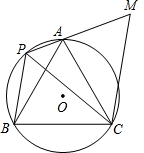 M∥BP交PA的延长线于点M.
M∥BP交PA的延长线于点M.