题目内容
已知等边△ABC内接于⊙O，点D是⊙O上任意一点，则sin∠ADB的值为（ ）| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
分析：先根据等边三角形的性质判断出∠ACB=60°，再由圆周角定理可知∠ADB的度数．根据特殊角的三角函数值即可求解．
解答：解：∵△ABC是等边三角形，∴∠ACB=60°．
∵∠ADB与∠ACB是同弧所对的圆周角，
∴∠ADB=60°．
∴sin∠ADB=sin60°=
．
故选C．
∵∠ADB与∠ACB是同弧所对的圆周角，
∴∠ADB=60°．
∴sin∠ADB=sin60°=
| ||
| 2 |
故选C．
点评：本题考查了等边三角形的性质、圆周角定理、特殊角的三角函数值，属较简单题目．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
已知等边△ABC内接于⊙O，点P是劣弧
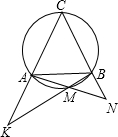如图，已知等边△ABC内接于圆，在劣弧AB上取异于A、B的点M，设直线AC与BM相交于K，直线CB与AM相交于点N，
上的一点（端点除外），延长BP至D，使BD=AP，连接CD．
