Question

如图，等边△ABC内接于⊙O，P是

AB

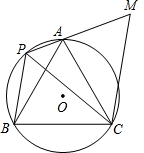上任一点（点P不与点A、B重合），连AP、BP，过点C作CM∥BP交PA的延长线于点M．
（1）填空：∠APC=

 

度，∠BPC=

 

度；
（2）求证：△ACM≌△BCP；
（3）若PA=1，PB=2，求梯形PBCM的面积．

Answer 1

分析：（1）利用同弧所对的圆周角相等即可求得题目中的未知角；
（2）利用上题中得到的相等的角和等边三角形中相等的线段证得两三角形全等即可；
（3）利用上题证得的两三角形全等判定△PCM为等边三角形，进而求得PH的长，利用梯形的面积公式计算梯形的面积即可．

解答：（1）解：∠APC=60°，∠BPC=60°；

（2）证明：∵CM∥BP，
∴∠BPM+∠M=180°，
∠PCM=∠BPC，
∵∠BPC=∠BAC=60°，
∴∠PCM=∠BPC=60°，
∴∠M=180°-∠BPM=180°-（∠APC+∠BPC）=180°-120°=60°，
∴∠M=∠BPC=60°，
又∵A、P、B、C四点共圆，
∴∠PAC+∠PBC=180°，
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC，
∴△ACM≌△BCP；

（3）解：作PH⊥CM于H，
∵△ACM≌△BCP，
∴CM=CP  AM=BP，
又∠M=60°，
∴△PCM为等边三角形，
∴CM=CP=PM=PA+AM=PA+PB=1+2=3，

在Rt△PMH中，∠MPH=30°，
∴PH=

3

2

3

，
∴S_梯形PBCM=

1

2

（PB+CM）×PH=

1

2

(2+3)×

3 3

2

=

15

4

3

．

点评：本题考查了圆周角定理、等边三角形的判定、全等三角形的性质及梯形的面积计算方法，是一道比较复杂的几何综合题．