题目内容
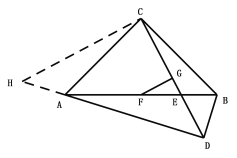
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC=8,点D在△ABC外,连接AD、BD,且∠ADB=90°,AB、CD相交于点E,AB、CD的中点分别是点F、G,连接FG.

(1)求AB的长;
(2)求证:AD+BD=![]() CD;
CD;
(3)若BD=6,求FG的值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)运用勾股定理即可求得AB的长;
(2)过点C作CH⊥CD,交DA的延长线于点H,然后再说明△ACH≌△BCD,最后利用勾股定理和线段的和差即可证明;
(3)取AD的中点K,连接FK、KG,进而说明FK、GK分别是△ABD、△DAC的中位线即可求得FK、GK的长;连接FD,由第(2)得AD+BD=![]() CD;连接CF,可知
CD;连接CF,可知![]() ;最后利用勾股定理解答即可.
;最后利用勾股定理解答即可.
(1)解:在Rt△ABC中
∴AB=![]() =
=![]() =
=![]()
(2)过点C作CH⊥CD,交DA的延长线于点H
∵∠ACB=90°,∠ADB=90°
∴∠CAD+∠CBD=360°-90°-90°=180°
∵∠CAD+∠CAH=180°
∴∠CBD=∠CAH
∵CH⊥CD,∠ACB=90°
∴∠ACH=∠BCD=90°-∠ACE
∵CA=CB
∴△ACH≌△BCD(ASA)
∴CH=CD,AH=DB
在Rt△HCD中
∴DH=![]() =
=![]() =
=![]()
∴AD+BD=AD+AH=DH=![]() CD.
CD.
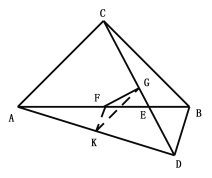
(3)解:取AD的中点K,连接FK、KG
∵K、F、G分别是AD、AB、CD的中点
∴FK、GK分别是△ABD、△DAC的中位线
∴![]() ,
,![]()
在△FGK中,GK-FK<FG<GK+FK,即4-3<FG<4+3,
∴1<FG<7.
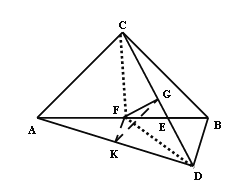
连接FD,由第(2)的:AD+BD=![]() CD
CD
∴![]() ,∴
,∴![]()
又![]()
连接CF,可知![]()
∴CF=DF
∴FG⊥CD
在Rt△FGD中,
![]() =
=![]() .
.


练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目







