题目内容
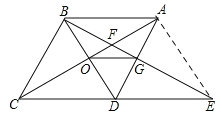
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于
交于![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() ,连结
,连结![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() 则下列结论:①
则下列结论:①![]() ;②与
;②与![]() 全等的三角形共有
全等的三角形共有![]() 个;③
个;③![]() ;④由点
;④由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形是菱形.其中正确的是( )
构成的四边形是菱形.其中正确的是( )

A.①④B.①③④C.①②③D.②③④
【答案】A
【解析】
连结![]() ,可说明四边形
,可说明四边形![]() 是平行四边形,即
是平行四边形,即![]() 是
是![]() 的中点;由有题意的可得O是BD的中点,即可判定①;运用菱形和平行四边形的性质寻找判定全等三角形的条件,找出与其全等的三角形即可判定②;证出OG是△ABD的中位线,得出OG//AB,OG=
的中点;由有题意的可得O是BD的中点,即可判定①;运用菱形和平行四边形的性质寻找判定全等三角形的条件,找出与其全等的三角形即可判定②;证出OG是△ABD的中位线,得出OG//AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形0DGF=S△ABF.即可判定③;先说明△ABD是等边三角形,则BD=AB,即可判定④.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形0DGF=S△ABF.即可判定③;先说明△ABD是等边三角形,则BD=AB,即可判定④.
解:如图:连结![]() .
.
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 是
是![]() 的中点,
的中点,
∵O是BD的中点
![]() ,①正确;
,①正确;
有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 个,②错误;
个,②错误;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG//AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∵△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△A0G的面积=△B0G的面积,
.∴![]() ;不正确;③错误;
;不正确;③错误;
![]()
![]() 是等边三角形.
是等边三角形.
![]() ,
,
![]() 是菱形,④正确.
是菱形,④正确.
故答案为A.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目