题目内容
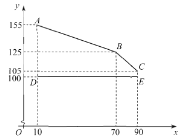
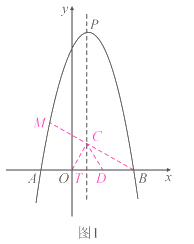
【题目】如图1,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)M为![]() 轴上方抛物线上的一点,
轴上方抛物线上的一点,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
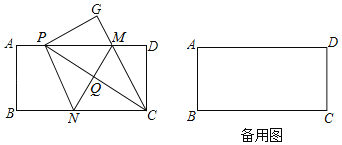
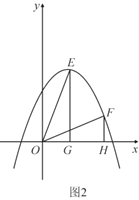
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为![]() ,
,![]() ,
,![]() 是新抛物线在第一象限内互不重合的两点,
是新抛物线在第一象限内互不重合的两点,![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,若始终存在这样的点
,若始终存在这样的点![]() ,
,![]() ,满足
,满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)点
;(2)点![]() 坐标为
坐标为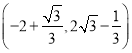 ;(3)
;(3)![]()
【解析】
(1)设![]() ,将点A的坐标代入求解即可;
,将点A的坐标代入求解即可;
(2)令![]() 求出点B的坐标,设抛物线对称轴直线
求出点B的坐标,设抛物线对称轴直线![]() 与
与![]() 轴交点为
轴交点为![]() ,作原点
,作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,根据已知条件可求出点C的坐标,根据待定系数法求出直线
,根据已知条件可求出点C的坐标,根据待定系数法求出直线![]() 的解析式,与抛物线解析式联立可求出点M的坐标;
的解析式,与抛物线解析式联立可求出点M的坐标;
(3)设![]() ,根据全等三角形的性质得出
,根据全等三角形的性质得出![]() ,设新抛物线解析式为
,设新抛物线解析式为![]() ,将点
,将点![]() 、
、![]() 的坐标代入抛物线的解析式得到两个等式,进而可得出m与n的关系,可先求出n的取值范围,最后根据h与n的函数关系式进行求解.
的坐标代入抛物线的解析式得到两个等式,进而可得出m与n的关系,可先求出n的取值范围,最后根据h与n的函数关系式进行求解.
解:(1)![]() 抛物线
抛物线![]() 的顶点为
的顶点为![]() ,
,
![]() ,
,
把![]() 代入抛物线解析式得,
代入抛物线解析式得,![]() ,
,
解得,![]() ,
,
![]() ;
;
(2)令![]() 得,
得,![]() ,
,
![]() 或
或![]() ,
,
![]() ,
,
![]() ,
,
设抛物线对称轴直线![]() 与
与![]() 轴交点为
轴交点为![]() ,作原点
,作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
与抛物线![]() 联立得
联立得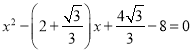 ,
,
![]() ,即
,即![]() ,
,
∴![]() ,
,
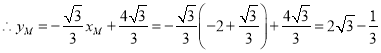 ,
,
故点![]() 坐标为
坐标为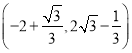 ;
;
(3)设![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设新抛物线解析式为![]() ,
,
把点![]() 、
、![]() 的坐标代入抛物线的解析式得:
的坐标代入抛物线的解析式得:![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
建立![]() 与
与![]() 或
或![]() 与
与![]() 的函数关系式,从而求
的函数关系式,从而求![]() 的取值范围,
的取值范围,
先找到![]() 与
与![]() 的关系式,
的关系式,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 且
且![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
![]() 且
且![]() ,
,
![]() ,
,
故![]() 的取值范围
的取值范围![]() .
.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目