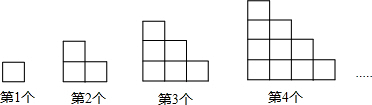
题目内容
10.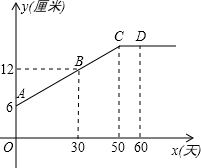 某生物小组观察一植物生长,得到植物高度y(单位:cm)与观察时间x(单位:天)的关系,并画出如图所示的图象(CD∥x轴)
某生物小组观察一植物生长,得到植物高度y(单位:cm)与观察时间x(单位:天)的关系,并画出如图所示的图象(CD∥x轴)(1)该植物从观察时起,多少天以后停止长高?
(2)求线段AC所在的直线解析式,并求该植物最高长多少厘米?
分析 (1)根据平行线间的距离相等可知50天后植物的高度不变,也就是停止长高;
(2)设直线AC的解析式为y=kx+b(k≠0),然后利用待定系数法求出直线AC线段的解析式,再把x=50代入进行计算即可得解.
解答 解:(1)∵CD∥x轴,
∴从第50天开始植物的高度不变,
答:该植物从观察时起,50天以后停止长高;
(2)设直线AC的解析式为y=kx+b(k≠0),
∵经过点A(0,6),B(30,12),
∴$\left\{\begin{array}{l}{b=6}\\{30k+b=12}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=6}\end{array}\right.$.
所以,直线AC的解析式为y=$\frac{1}{5}$x+6(0≤x≤50),
当x=50时,y=$\frac{1}{5}$×50+6=16cm.
答:直线AC所在线段的解析式为y=$\frac{1}{5}$x+6(0≤x≤50),该植物最高长16cm.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知自变量求函数值,仔细观察图象,准确获取信息是解题的关键.

练习册系列答案
相关题目
20. 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )
 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )| A. | $y=\frac{20}{x}$ | B. | $y=-\frac{20}{x}$ | C. | $y=\frac{12}{x}$ | D. | $y=-\frac{12}{x}$ |
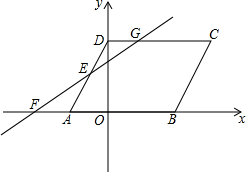 在平面直角坐标系中,O是坐标原点,平行四边形ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,2$\sqrt{3}$),且AB:AD=3:2,点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线与x轴交于点F(-4,0),与DC交于点G.
在平面直角坐标系中,O是坐标原点,平行四边形ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,2$\sqrt{3}$),且AB:AD=3:2,点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线与x轴交于点F(-4,0),与DC交于点G.