题目内容
1．下列函数中，是二次函数的是（ ）| A． | y=1-x | B． | y=（x-1）2-x2 | C． | y=-$\frac{1}{x}$ | D． | y=-x2 |
分析 根据形如y=ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数，可得答案．
解答 解：A、y=1-x是一次函数，故A错误；
B、y=（x-1）2-x2是一次函数，故B错误；
C、y=-$\frac{1}{x}$是反比例函数，故C错误；
D、y=-x2是二次函数，故D正确；
故选：D．
点评 本题考查了二次函数的定义，形如y=ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．
练习册系列答案
相关题目
9．在一次“构造勾股数”的探究性学习中，老师给出了下表：
其中m、n为正整数，且m＞n．
（1）观察表格，当m=2，n=1时，此时对应的a、b、c的值能否为直角三角形三边的长？说明你的理由．
（2）探究a，b，c与m、n之间的关系并用含m、n的代数式表示：a=m2+n2，b=2mn，c=m2-n2．
（3）以a，b，c为边长的三角形是否一定为直角三角形？如果是，请说明理由；如果不是，请举出反例．
| m | 2 | 3 | 3 | 4 | … |
| n | 1 | 1 | 2 | 3 | … |
| a | 22+12 | 32+12 | 32+22 | 42+32 | … |
| b | 4 | 6 | 12 | 24 | … |
| c | 22-12 | 32-12 | 32-22 | 42-32 | … |
（1）观察表格，当m=2，n=1时，此时对应的a、b、c的值能否为直角三角形三边的长？说明你的理由．
（2）探究a，b，c与m、n之间的关系并用含m、n的代数式表示：a=m2+n2，b=2mn，c=m2-n2．
（3）以a，b，c为边长的三角形是否一定为直角三角形？如果是，请说明理由；如果不是，请举出反例．
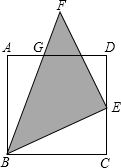如图，点E是正方形ABCD的CD边上的一点，以BE为一条直角边作等腰直角三角形BEF，斜边BF交AD于G，已知AG=5厘米，GD=15厘米．三角形BEF的面积是272厘米2．