题目内容
5.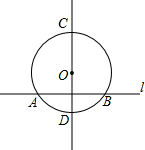 如图,已知⊙O的半径为5cm,直线CD经过圆心O,直线l与直线CD垂直,交⊙O于A、B两点,且AB=8cm.如果直线l与⊙O相切,那么直线l应平移2cm或8cm.
如图,已知⊙O的半径为5cm,直线CD经过圆心O,直线l与直线CD垂直,交⊙O于A、B两点,且AB=8cm.如果直线l与⊙O相切,那么直线l应平移2cm或8cm.
分析 首先连接OA,由垂径定理即可求得AE的长,然后由勾股定理求得OE的长,继而求得答案.
解答 解:连接OA,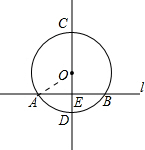
∵⊙O的半径为5cm,
∴OA=5cm,
∵直线l⊥AB,
∴AE=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4(cm),
∴OE=$\sqrt{A{O}^{2}-A{E}^{2}}$=3(cm),
∴DE=OD-OE=5-3=2(cm),CE=OC+OE=8(cm),
即直线l沿半径CD向下平移2cm时或向上平移8cm与⊙O相切.
故答案为:2cm或8cm.
点评 此题考查了切线的性质、垂径定理以及勾股定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
15.下面4个点中,哪个点在直线y=-2x+3上( )
| A. | (-1,1) | B. | (1,-1) | C. | (2,-1) | D. | (5,13) |
10.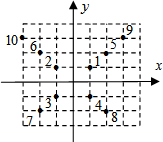 如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
 如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )
如图,在一坐标平面上,1在(1,1)位置,将自然数由小到大,由内而外,依逆时针方向排列在正方形的各顶点,那么数字159的位置在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.在式子:①(x-1)0,②$\sqrt{x-1}$,③$\frac{1}{x-1}$中,x可以取1的是( )
| A. | ①和② | B. | 只有① | C. | 只有② | D. | 只有③ |
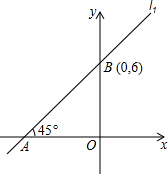 如图,平面直角坐标系中画出了函数l1:y1=kx+b的图象.
如图,平面直角坐标系中画出了函数l1:y1=kx+b的图象.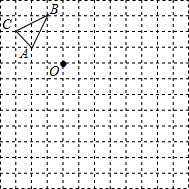 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点O.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点O.