题目内容
10.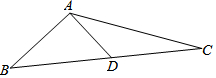 如图,已知在△ABC中,AB=3,AC=5,则BC边上的中线AD=2,则BC=2$\sqrt{13}$.
如图,已知在△ABC中,AB=3,AC=5,则BC边上的中线AD=2,则BC=2$\sqrt{13}$.
分析 延长AD到E,使DE=AD,连接BE,如图所示,由D为BC的中点,得到CD=BD,再由一对对顶角相等,利用SAS得出三角形ACD与三角形EDB全等,由全等三角形的对应边相等得到BE=AC=5,由AE=2AD=4,AB=5,利用勾股定理的逆定理得到三角形ABE为直角三角形,再利用勾股定理求出BD即可解决问题.
解答 解:延长AD到E,使得AD=DE,连接BE.
在△ADC和△EDB中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠BDE}\\{DC=BD}\end{array}\right.$,
∴△ADC≌△EDB,
∴∴AC=BE=5,
∵AB=2,AE=4,BE=5,
∴AB2+AE2=BE2,
∴∠BAE=90°,
∴BD=DC=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{13}$,
∴BC=2BD=2$\sqrt{13}$.
故答案为2$\sqrt{13}$
点评 此题考查了勾股定理及逆定理,以及全等三角形的判定与性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
5.如图所示的是一个数值转换机,若输入的a值为-4,则输出的结果为( )


| A. | -34 | B. | -30 | C. | 30 | D. | 34 |
15.某年的7月份有5个星期六,并且它们的日期之和为85,则7月4日是( )
| A. | 星期四 | B. | 星期五 | C. | 星期六 | D. | 星期日 |
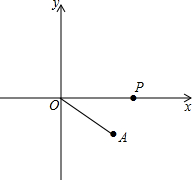 有这样一个问题:如图,坐标平面内一点A(2,-1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,求符合条件的动点P的个数.小岚是这样解决的:
有这样一个问题:如图,坐标平面内一点A(2,-1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,求符合条件的动点P的个数.小岚是这样解决的: (1)计算:($\sqrt{3}$-1)0+2sin30°-($\frac{1}{2}$)-1+|-2017|;
(1)计算:($\sqrt{3}$-1)0+2sin30°-($\frac{1}{2}$)-1+|-2017|;