题目内容
5.已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{-3x+y=2}\\{4x+y=5}\end{array}\right.$的解,则a+2b的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 首先把方程组的解$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{-3x+y=2}\\{4x+y=5}\end{array}\right.$,得到一个关于a,b的方程组,即可求得代数式的值.
解答 解:把$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{-3x+y=2}\\{4x+y=5}\end{array}\right.$,
可得:$\left\{\begin{array}{l}{-3a+b=2}\\{4a+b=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{7}}\\{b=\frac{23}{7}}\end{array}\right.$,
则a+2b=7,
故选D
点评 本题主要考查了方程组的解的定义:能使方程组中每个方程的左右两边相等的未知数的值即是方程组的解.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
13.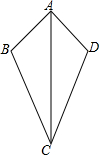 如图:①AB=AD.②∠B=∠D,③∠BAC=∠DAC,④BC=DC,以上4等式中的2个等式不能作为依据来证明△ABC≌△ADC的是( )
如图:①AB=AD.②∠B=∠D,③∠BAC=∠DAC,④BC=DC,以上4等式中的2个等式不能作为依据来证明△ABC≌△ADC的是( )
 如图:①AB=AD.②∠B=∠D,③∠BAC=∠DAC,④BC=DC,以上4等式中的2个等式不能作为依据来证明△ABC≌△ADC的是( )
如图:①AB=AD.②∠B=∠D,③∠BAC=∠DAC,④BC=DC,以上4等式中的2个等式不能作为依据来证明△ABC≌△ADC的是( )| A. | ①,② | B. | ①,③ | C. | ①,④ | D. | ②,③ |
15. 用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
 用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
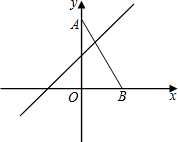 已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).
已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).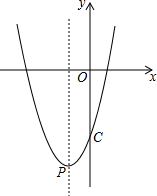 已知二次函数y=x2+bx-4的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=$\frac{1}{4}$
已知二次函数y=x2+bx-4的图象与y轴的交点为C,与x轴正半轴的交点为A,且tan∠ACO=$\frac{1}{4}$ 如图是某教室里日光灯的四个控制开关(分别记为A、B、C、D),每个开关分别控制一排日光灯(开关序号与日光灯的排数序号不一定一致).某天上课时,王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关.
如图是某教室里日光灯的四个控制开关(分别记为A、B、C、D),每个开关分别控制一排日光灯(开关序号与日光灯的排数序号不一定一致).某天上课时,王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关. 如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是30°.
如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是30°.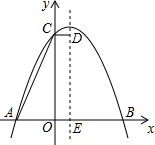 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,则下列结论正确的序号为①③④(多填或错填得0分,少填酌情给分)
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,则下列结论正确的序号为①③④(多填或错填得0分,少填酌情给分)