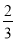题目内容
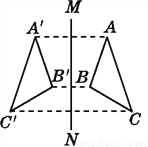
如图,已知△A'B'C'与△ABC关于直线MN对称,则MN垂直平分__________.
 AA',BB',CC'
【解析】已知△ABC与△A′B′C′关于直线MN对称,根据轴对称的性质,对应点的连线被对称轴垂直平分可得MN垂直平分线段AA′、线段BB′、线段CC′.
故答案为:线段AA′、线段BB′、线段CC′.
AA',BB',CC'
【解析】已知△ABC与△A′B′C′关于直线MN对称,根据轴对称的性质,对应点的连线被对称轴垂直平分可得MN垂直平分线段AA′、线段BB′、线段CC′.
故答案为:线段AA′、线段BB′、线段CC′.
练习册系列答案
相关题目
一项工程,甲单独做需要x小时完成,乙单独做需要y小时完成,则两人一起完成这项工程需要_______小时.
 【解析】设该工程总量为1.二人合作完成该工程所需天数=1÷(=.
【解析】设该工程总量为1.二人合作完成该工程所需天数=1÷(=. 根据变化完成式子的变形: 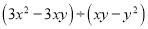 =3x÷_____.
=3x÷_____.
 y
【解析】因为,故答案为: y.
y
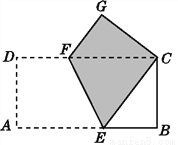
【解析】因为,故答案为: y. 如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)试说明:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
 (1)见解析;(2)16
【解析】试题分析:(1)先证∠GCF=∠BCE,根据折叠性质,GC=AD=BC,∠G=∠D=∠B=90°根据ASA判定全等即可;(2)由(1)可知,阴影面积=四边形BCFE面积=矩形面积的一半,计算即可.
试题解析:
(1)因为∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
所以∠GCF=∠BCE.
又因为∠G=∠B=90°,GC=...
(1)见解析;(2)16
【解析】试题分析:(1)先证∠GCF=∠BCE,根据折叠性质,GC=AD=BC,∠G=∠D=∠B=90°根据ASA判定全等即可;(2)由(1)可知,阴影面积=四边形BCFE面积=矩形面积的一半,计算即可.
试题解析:
(1)因为∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
所以∠GCF=∠BCE.
又因为∠G=∠B=90°,GC=... 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
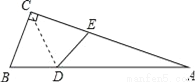
A. 44° B. 60° C. 67° D. 77°
 C
【解析】试题分析:由∠ACB=90°,∠A=22°,三角形内角和是180º,可得∠B=90º-22º=68º,因为折叠角相等,所以∠CED=∠B=68º,∠BDC=∠EDC=∠BDE,,因为四边形内角和是360º,所以∠BDE=360º-90º-68º-68º=134º,所以∠BDC=∠BDE=×134º=67º.故选C.
C
【解析】试题分析:由∠ACB=90°,∠A=22°,三角形内角和是180º,可得∠B=90º-22º=68º,因为折叠角相等,所以∠CED=∠B=68º,∠BDC=∠EDC=∠BDE,,因为四边形内角和是360º,所以∠BDE=360º-90º-68º-68º=134º,所以∠BDC=∠BDE=×134º=67º.故选C. 

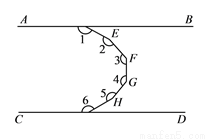
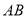 、
、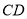 平行,则
平行,则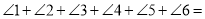 ( ).
( ).
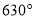 B.
B. 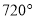 C.
C. 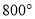 D.
D. 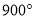
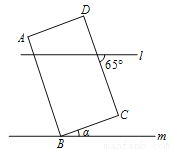
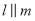 ,长方形
,长方形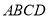 的顶点
的顶点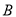 在直线
在直线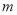 上,则
上,则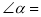 _________.
_________.
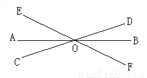
 的对顶角是___,∠COF的邻补角是_____,若
的对顶角是___,∠COF的邻补角是_____,若 :
:  =2:3,
=2:3,  ,则
,则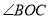 =_____.
=_____.
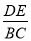 的值为( )
的值为( )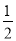 B.
B. 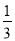 C.
C. 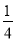 D.
D.