题目内容
9.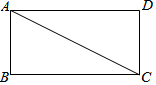 如图,已知在矩形ABCD中,AB=4,AD=8,将△ABC沿对角线AC翻折,点B落在点E处,联结DE,则DE的长为$\frac{12}{5}$$\sqrt{5}$.
如图,已知在矩形ABCD中,AB=4,AD=8,将△ABC沿对角线AC翻折,点B落在点E处,联结DE,则DE的长为$\frac{12}{5}$$\sqrt{5}$.
分析 先过E作EF⊥AD于F,设CG=Ax,则DG=8-x,在Rt△CDG中,根据DG2+CD2=CG2,得到(8-x)2+42=x2,求得AG=5,再根据EF=$\frac{AE×EG}{AG}$=$\frac{12}{5}$,运用勾股定理求得AF和DF的长,即可得到DE的长.
解答  解:如图所示,过E作EF⊥AD于F,
解:如图所示,过E作EF⊥AD于F,
由折叠可得,∠ACB=∠ACE,
∵AD∥BC,
∴∠ACB=∠CAD,
∴∠CAD=∠ACE,
∴CG=AG,
设CG=Ax,则DG=8-x,
∵Rt△CDG中,DG2+CD2=CG2,
∴(8-x)2+42=x2,
解得x=5,
∴AG=5,
∴Rt△AEG中,EG=$\sqrt{A{G}^{2}-A{E}^{2}}$=3,
∵EF⊥AG,∠AEG=90°,
∴EF=$\frac{AE×EG}{AG}$=$\frac{12}{5}$,
∴Rt△AEF中,AF=$\sqrt{A{E}^{2}-E{F}^{2}}$=$\frac{16}{5}$,
∴DF=8-$\frac{16}{5}$=$\frac{24}{5}$,
∴Rt△DEF中,DE=$\sqrt{E{F}^{2}+D{F}^{2}}$=$\frac{12}{5}\sqrt{5}$.
故答案为:$\frac{12}{5}\sqrt{5}$.
点评 本题属于折叠问题,主要考查了矩形的性质,勾股定理的综合应用,解题时注意面积法以及方程思想的运用.本题也可以运用相似三角形的性质进行求解.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19.中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为P=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(kg)与时间t(天)的关系如表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
14.下列说法中,正确的是( )
| A. | 一组数据-2,-1,0,1,1,2的中位数是0 | |
| B. | 质检部门要了解一批灯泡的使用寿命,应当采用普查的调查方式 | |
| C. | 购买一张福利彩票中奖是一个确定事件 | |
| D. | 分别写有三个数字-1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为$\frac{1}{3}$ |
 如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC. 已知二次函数y=x2+(2m-2)x+m2-2m-3(m是常数)的图象与x轴交于A,B两点(点A在点B的左边).
已知二次函数y=x2+(2m-2)x+m2-2m-3(m是常数)的图象与x轴交于A,B两点(点A在点B的左边).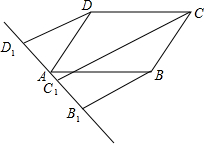 如图,直线l过?ABCD的顶点A,点D1、C1、B1都在直线l上,且DD1∥CC1∥BB1,求证:CC1=DD1+BB1.
如图,直线l过?ABCD的顶点A,点D1、C1、B1都在直线l上,且DD1∥CC1∥BB1,求证:CC1=DD1+BB1.