Question

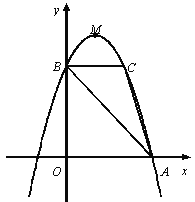
【题目】如图，抛物线y＝ax 2＋bx＋c的顶点为M（1，4），与x轴的右交点为A，与y轴的交点为B，点C与点B关于抛物线的对称轴对称，且S△ABC ＝3．

（1）求抛物线的解析式；

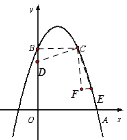
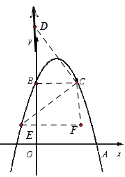
（2）点D是y轴上一点，将点D绕C点逆时针旋转90°得到点E，若点E恰好落在抛物线上，请直接写出点D的坐标；

（3）设抛物线的对称轴与直线AB交于点F，问：在x轴上是否存在点P，使得以P、A、F为顶点的三角形与△ABC相似？若存在，求点P的坐标；若不存在，请说明理由

Answer 1

【答案】（1）抛物线的解析式为y＝－x 2＋2x＋3 （或写顶点式 ）；（2）D（0，4+）或（0，4-）；；（3）P1（，0）P2（－3，0）

【解析】试题分析：（1）根据B、C是对称点确定BC=2，然后再根据面积确定OB的长，从而确定出点B坐标，再利用待定系数法即可求得解析式；

（2）设D（0，d），然后根据旋转的性质确定出点E坐标，由点E在抛物线上，代入进行求解即可得；

（3）根据题意画出所有满足条件的图形，然后分情况进行求解即可.

试题解析：(1）由题意可知对称轴为x=1，点B在y轴上，点B与点C是对称点，所以BC=2，

又S△ABC ＝=3，所以OB＝3，所以点B（0，3），

设抛物线的解析式为：y=a（x-1）2+4，

∵点B的坐标为（0，3），

∴a+4=3，

∴a=-1，

∴此抛物线的解析式为：y=-（x-1）2+4=-x2+2x+3；

（2）由点B与点C是对称点，所以点C（2，3），

如图，设点D（0，d），有如下两种情况，则有BD=|3-d|，

由已知易得△CBD≌△CFE，∴CF=CB=2，EF=BD=|3-d|，

所以E（5-d，1），

由点E恰好落在抛物线上，则有：1=-（5-d-1）2+4，

解得：d=4±，

所以D（0，4+）或（0，4-）；

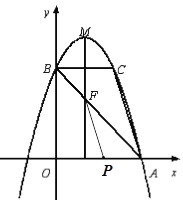
（3）令y=0，0=-（x-1）2+4，解得：x=3或x=-1，

所以A（3，0），

因为B（0，3），所以OA＝OB，所以∠BAO=45°，AB=3，

∵BC//OA，∴∠CBA=∠BAO=45°，

∵对称轴为x=1，∴F（1，2），AF=2 ，

如图，若△PAF∽△CAB，则有PA：CB=AF：AB，∴PA=，

∴OP=OA-PA=，∴P（，0）；

如图，若△PAF∽△ABC，则有PA：AB=AF：BC，∴PA=6，

∴OP=PA-AO=3，∴P（-3，0），

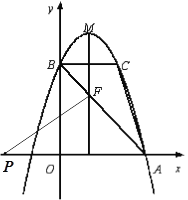
综上，P1（，0），P2（-3，0）.