Question

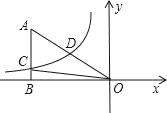
【题目】如图，在矩形ABCD中，AB＝6，AD＝8，矩形内一动点P使得S△PAD＝S矩形ABCD，则点P到点A、D的距离之和PA+PD的最小值为_____．

Answer 1

【答案】8

【解析】

根据S△PAD＝S矩形ABCD，得出动点P在与AD平行且与AD的距离是4的直线l上，作A关于直线l的对称点E，连接DE，BE，则DE的长就是所求的最短距离．然后在直角三角形ADE中，由勾股定理求得DE的值，即可得到PA+PD的最小值．

设△PAD中AD边上的高是h．

∵S△PAD＝S矩形ABCD，

∴ ADh＝ADAB，

∴h＝AB＝4，

∴动点P在与AD平行且与AD的距离是4的直线l上，

如图，作A关于直线l的对称点E，连接BE，DE，则DE的长就是所求的最短距离．

在Rt△ADE中，∵AD＝8，AE＝4+4＝8，

DE＝ ,

即PA+PD的最小值为8 ．

故答案8．