题目内容
若a>0,b>0,c>0,b2-4ac>0,则抛物线y=ax2+bx+c不经过第 象限.
考点:二次函数图象与系数的关系
专题:数形结合
分析:由a>0得到抛物线开口向上,则抛物线必过第一、二象限,再由a、b同号得到抛物线的对称轴在y轴的左侧,由c>0得抛物线与y轴的交点在x轴上方,则抛物线不经过第四象限,接着由b2-4ac>0得抛物线与x轴有2个交点,则抛物线的顶点在第三象限,所以抛物线y=ax2+bx+c不经过第四象限.
解答:解:∵a>0,
∴抛物线开口向上,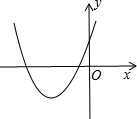
∵b>0,
∴抛物线的对称轴在y轴的左侧,
∵c>0,
∴抛物线与y轴的交点在x轴上方,
∵b2-4ac>0,
∴抛物线与x轴有2个交点,
抛物线的大致位置如图所示,
∴抛物线y=ax2+bx+c不经过第四象限.
故答案为四.
∴抛物线开口向上,

∵b>0,
∴抛物线的对称轴在y轴的左侧,
∵c>0,
∴抛物线与y轴的交点在x轴上方,
∵b2-4ac>0,
∴抛物线与x轴有2个交点,
抛物线的大致位置如图所示,
∴抛物线y=ax2+bx+c不经过第四象限.
故答案为四.
点评:本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
点A为数轴上表示-2的点,当点A沿数轴移动4个单位长到B时,点B所表示的数是( )
| A、1 | B、-6 | C、2或-6 | D、2 |
下列说法不正确的是( )
| A、互为相反数的两个数的绝对值相等 |
| B、一个数的绝对值越大,表示它的点在数轴上离原点越远 |
| C、一个数的绝对值越大,表示它的点在数轴上越靠右 |
| D、一个负数的绝对值越大,表示它的点在数轴上越靠左 |

 如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积为3,那么△PDC与△PAB的面积和等于
如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积为3,那么△PDC与△PAB的面积和等于 如图,△ABC与△A′B′C′关于某一点成中心对称,画出对称中心.
如图,△ABC与△A′B′C′关于某一点成中心对称,画出对称中心.