题目内容
在一个平面内任意画出6条直线,最多可以把平面分成几个部分?n条直线呢?
考点:直线、射线、线段
专题:规律型
分析:根据每两条直线都相交且三条直线不交于同一点,可得最多平面.先分别求得1条,2条,3条直线,4条直线,直线两两相交最多可将平面分割成的区域个数,总结规律,进而求解.
解答:解:1条直线时,平面最多被分为1+1=2部分;
2条直线时,平面最多被分为1+1+2=4部分;
3条直线时,平面最多被分为1+1+2+3=7部分;
4条直线时,平面最多被分为1+1+2+3+4=11部分;
5条直线时,平面最多被分为1+1+2+3+4+5=16部分
可知:6条直线时:平面最多被分为1+1+2+3+4+5+6=22部分
n条直线时:平面最多可分为:1+1+2+3+4+…+n=1+(1+2+3+4+…+n)=1+
=
(部分).
2条直线时,平面最多被分为1+1+2=4部分;
3条直线时,平面最多被分为1+1+2+3=7部分;
4条直线时,平面最多被分为1+1+2+3+4=11部分;
5条直线时,平面最多被分为1+1+2+3+4+5=16部分
可知:6条直线时:平面最多被分为1+1+2+3+4+5+6=22部分
n条直线时:平面最多可分为:1+1+2+3+4+…+n=1+(1+2+3+4+…+n)=1+
| n(n+1) |
| 2 |
| n2+n+2 |
| 2 |
点评:本题考查了直线、射线、线段,每两条直线都相交且三条直线不交于同一点,可得最多平面,计算、观察、发现规律是解题关键.

练习册系列答案
相关题目
将y=3x2的图象向右平移1个单位,再向上平移3个单位,得到的抛物线的解析式为( )
| A、y=3(x-1)2-3 |
| B、y=3(x+1)2+3 |
| C、y=3(x+1)2-3 |
| D、y=3(x-1)2+3 |
在0,-
,
,0.1010010001…,
这五个数中,是无理数的有( )个.
| 1 |
| 3 |
| 9 |
| π |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
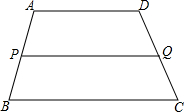 如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DCC于Q点
如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DCC于Q点 如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,求证:DE=3BE.
如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,求证:DE=3BE.