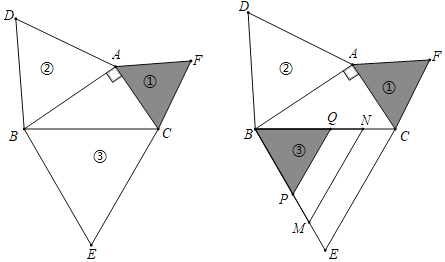
题目内容
【题目】定义:在平面直角坐标系中,对于任意两点![]() , ,当点
, ,当点![]() 满足
满足![]() , 时,则称点
, 时,则称点![]() 为点
为点![]() ,的“四合点”.例如:
,的“四合点”.例如:![]() ,当点
,当点![]() 满足
满足![]() ,则点
,则点![]() 为点
为点![]() ,的“四合点”.
,的“四合点”.
![]() 若点
若点![]() ,则点
,则点![]() 的“四合点” 的坐标为
的“四合点” 的坐标为
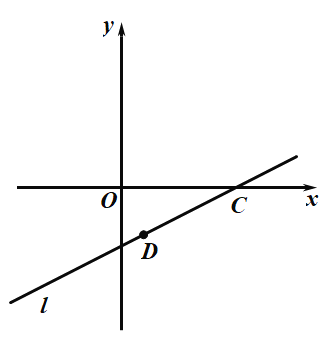
![]() 如图,点
如图,点![]() ,点
,点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 为点
为点![]() 的“四合点”,
的“四合点”,
①请求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②已知点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与
与![]() 相似,若存在,请求出此时点
相似,若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]()
![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)根据“四合点”定义直接解得;(2)①根据“四合点”定义用t表示出T点坐标,再用x表示出t,代入y即可得到函数关系式;②根据E、C点坐标易知△OEC为等边三角形,即可得到△CTO也为等边三角形,又可根据![]() 得到OQ=ET,再根据垂直平分线可得到
得到OQ=ET,再根据垂直平分线可得到![]() ,进而得到OT解析式,再通过交点解得T,进而得到D点坐标.
,进而得到OT解析式,再通过交点解得T,进而得到D点坐标.
![]() 若点
若点![]() ,
,
则点![]() 的“四合点”
的“四合点” ![]() 的坐标为
的坐标为![]()
![]() ①
①![]() 点
点![]() 为
为![]() 与点
与点![]() 的四合点
的四合点
![]()
![]()
![]()
![]()
②如图
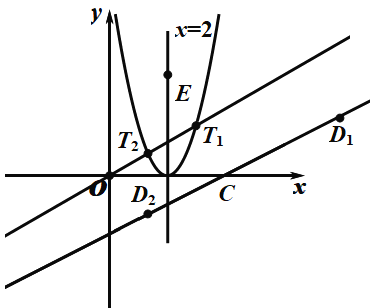
![]()
![]() 为等边三角形
为等边三角形
又![]() 与
与![]() 相似
相似
![]() 为等边三角形
为等边三角形
![]()
![]()
![]()
又![]() 直线
直线![]() 垂直平分
垂直平分![]() ,
,
且点![]() 为直线
为直线 ![]() 上一点
上一点
![]()
![]()
![]() 垂直平分
垂直平分![]()
![]() 直线
直线![]()
令![]() ,
,
解得![]()
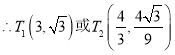
![]()

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目