题目内容
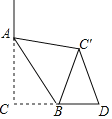
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内一个动点,且满足
内一个动点,且满足![]() ,当线段
,当线段![]() 取最小值时,记
取最小值时,记![]() ,线段
,线段![]() 上一动点
上一动点![]() 绕着点
绕着点![]() 顺时针旋转得到点
顺时针旋转得到点![]() ,且满足
,且满足![]() ,则
,则![]() 的最小值为 _____________
的最小值为 _____________
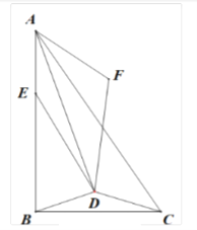
【答案】![]()
【解析】
先确定CD最小时,点D的位置,将DA绕点D逆时针旋转![]() ,得到DG,连接GE,利用SAS即可证出△GDE≌△ADF,从而得出GE=AF,可得当GE⊥AB时,GE最小,即AF最小,然后过点D作DM⊥AB于M,过点G作GH⊥DM交DM的延长线于H,利用相似三角形的判定及性质和全等三角形的判定及性质即可求出结论.
,得到DG,连接GE,利用SAS即可证出△GDE≌△ADF,从而得出GE=AF,可得当GE⊥AB时,GE最小,即AF最小,然后过点D作DM⊥AB于M,过点G作GH⊥DM交DM的延长线于H,利用相似三角形的判定及性质和全等三角形的判定及性质即可求出结论.
解:∵![]() ,
,
∴∠DBC+∠ABD=90°
∵![]() ,设
,设![]() =
=![]()
∴∠DAB+∠ABD=90°
∴∠ADB=90°
∴点D在以AB为直径的圆上,设圆心为O,半径为![]() ,易知当O、D、C三点共线时CD最小,
,易知当O、D、C三点共线时CD最小,
∴OD=OB=OA=3,
∴OC=![]()
将DA绕点D逆时针旋转![]() ,得到DG,连接GE,
,得到DG,连接GE,
∴DG=DA,∠GDA=∠EDF=![]()
∴∠GDE=∠ADF
∵DE=DF
∴△GDE≌△ADF
∴GE=AF
∴当GE⊥AB时,GE最小,即AF最小
过点D作DM⊥AB于M,过点G作GH⊥DM交DM的延长线于H
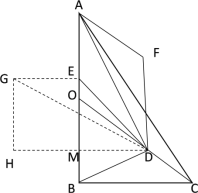
∴DM∥BC,四边形GHME为矩形
∴△OMD∽△OBC,GE=HM
∴![]()
即![]()
∴DM=![]() ,OM=
,OM=![]()
∴AM=OM+OA=![]()
∵![]() =
=![]() ,OA=OD
,OA=OD
∴∠ODA=∠OAD=![]()
∴∠BOC=∠ODA+∠OAD=2![]()
在Rt△OBC中,∠OCB=90°-∠BOC
即![]() =90°-2
=90°-2![]()
∵∠MAD+∠MDA=90°
∴![]() +
+![]() +∠GDH=90°
+∠GDH=90°
∴![]() +90°-2
+90°-2![]() +∠GDH=90°
+∠GDH=90°
∴∠GDH=![]() =∠DAM
=∠DAM
∵∠DHG=∠AMD=90°,AD=DG
∴△GDH≌△DAM
∴DH=AM=![]()
∴HM=DH-DM=![]()
∴AF=GE=HM=![]()
即AF的最小值为![]()
故答案为:![]() .
.

 寒假乐园北京教育出版社系列答案
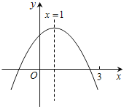
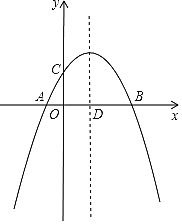
寒假乐园北京教育出版社系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论错误的是( )
A.ac<0
B.当x>1时,y的值随x的增大而减小
C.3是方程ax2+(b﹣1)x+c=0的一个根
D.当﹣1<x<3时,ax2+(b﹣1)x+c>0