题目内容
12.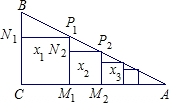 如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…xn的n个正方形依次放在△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…其他正方形依次放入,则第2016个正方形的边长X2016为($\frac{2}{3}$)2016.
如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…xn的n个正方形依次放在△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…其他正方形依次放入,则第2016个正方形的边长X2016为($\frac{2}{3}$)2016.
分析 由四边形CDEF是正方形,即可得CD=CF=DE=EF=x1,DE∥AC,然后根据平行线分线段成比例定理,即可得 $\frac{{N}_{1}{P}_{1}}{AC}$,又由BC=1,AC=2,即可求得x1的值,同理求得x2,x3的值;
观察规律即可求得第n个正方形的边长xn=( $\frac{2}{3}$)n.
解答  解:如图,∵四边形CM1P1N1是正方形,
解:如图,∵四边形CM1P1N1是正方形,
则CN1=CM1=P1N1=M1P=x1,P1N1∥AC,
∴$\frac{{N}_{1}{P}_{1}}{AC}$=$\frac{B{N}_{1}}{BC}$,
即$\frac{{x}_{1}}{1}$=$\frac{2-{x}_{1}}{2}$,
∴x1=$\frac{2}{3}$,
同理:x2=($\frac{2}{3}$)2,
x3=($\frac{2}{3}$)3,
…
∴xn=($\frac{2}{3}$)n.
∴x2016=($\frac{2}{3}$)2016.
故答案为:($\frac{2}{3}$)2016.
点评 此题考查了正方形的性质,平行线分线段成比例定理,考查了学生的观察归纳能力.此题难度适中,解题的关键是数形结合思想与方程思想的应用.

练习册系列答案
相关题目
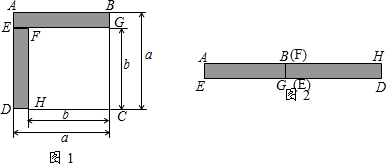
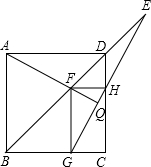 已知:正方形ABCD中,F为BD上任意一点,过点F作FH⊥CD于点H,FG⊥BC于点G,连接AF并延长交GH于点Q,延长BD、GH交于点E.
已知:正方形ABCD中,F为BD上任意一点,过点F作FH⊥CD于点H,FG⊥BC于点G,连接AF并延长交GH于点Q,延长BD、GH交于点E.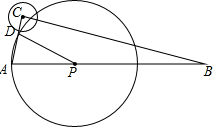 如图,在Rt△ABC中,∠ACB=90°,AC=4,cosA=$\frac{1}{4}$,点P是AB上的动点,以PA为半径作⊙P.若⊙C的半径等于1,且⊙P与⊙C的公共弦长为$\sqrt{2}$,求AP的长.
如图,在Rt△ABC中,∠ACB=90°,AC=4,cosA=$\frac{1}{4}$,点P是AB上的动点,以PA为半径作⊙P.若⊙C的半径等于1,且⊙P与⊙C的公共弦长为$\sqrt{2}$,求AP的长.