题目内容
2.已知,AB∥CD,MN分别交AB、CD于E、F.(1)如图1,若EG平分∠AEN,FH平分∠CFE,判定EG与FH的位置关系并证明;
(2)如图2,若∠AEF和∠EFC的角平分线交于点P,求∠EPF.
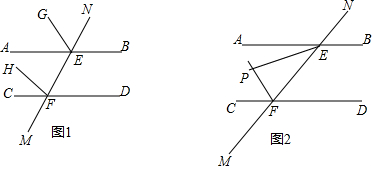
分析 (1)由角平分线得∠GEN=$\frac{1}{2}$∠AEN、∠HFE=$\frac{1}{2}$∠CFE,根据AB∥CD知∠AEN=∠CFE,从而得出∠GEN=∠HFE,即可得证;
(2)由AB∥CD知∠AEF+∠CFE=180°,根据角平分线知∠PEF+∠PFE=$\frac{1}{2}$(∠AEF+∠CFE)=90°,再由三角形内角和定理可得答案.
解答 解:(1)∵EG平分∠AEN,FH平分∠CFE,
∴∠GEN=$\frac{1}{2}$∠AEN、∠HFE=$\frac{1}{2}$∠CFE,
∵AB∥CD,
∴∠AEN=∠CFE,
∴∠GEN=∠HFE,
∴GE∥HF;
(2)∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵EP平分∠AEF、FP平分∠CFE,
∴∠PEF+∠PFE=$\frac{1}{2}$∠AEF+$\frac{1}{2}$∠CFE=$\frac{1}{2}$(∠AEF+∠CFE)=90°,
∴∠EPF=180°-(∠PEF+∠PFE)=90°.
点评 本题主要考查平行线的性质,熟练掌握平行线的性质、角平分线的性质及三角形的内角和定理是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
12. 为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( )
为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( )
 为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( )
为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( )| A. | 12 | B. | 12.5 | C. | 13 | D. | 14 |
10.下列四个实数中,无理数是( )
| A. | 0 | B. | $\frac{22}{7}$ | C. | -2 | D. | $\sqrt{3}$ |
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EFC=$\frac{12}{5}$.其中正确结论的是①②③④(只填序号).
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EFC=$\frac{12}{5}$.其中正确结论的是①②③④(只填序号). 如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=2,则菱形ABCD的周长是16.
如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=2,则菱形ABCD的周长是16. 如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a、b均为正整数,则C点的坐标为(5,1),(1,3),(3,4),(5,5).
如图,在直角坐标系中,△ABC的面积为2,三个顶点的坐标分别为A(3,2),B(1,1),C(a,b),且a、b均为正整数,则C点的坐标为(5,1),(1,3),(3,4),(5,5).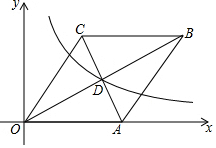 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y=$\frac{k}{x}$的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为2.
如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y=$\frac{k}{x}$的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为2.