题目内容
18.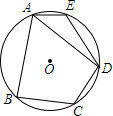 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在$\widehat{AD}$上.
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在$\widehat{AD}$上.(1)求∠AED的度数;
(2)若⊙O的半径为2,则$\widehat{AD}$的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.
分析 (1)连接BD,根据圆的内接四边形的性质得出∠BAD的度数,由AB=AD,可证得△ABD是等边三角形,求得∠ABD=60°,再利用圆的内接四边形的性质,即可求得∠E的度数;
(2)连接OA,由圆周角定理求出∠AOD的度数,由弧长公式即可得出$\widehat{AD}$的长;
(3)首先连接OA,由∠ABD=60°,利用圆周角定理,即可求得∠AOD的度数,继而求得∠AOE的度数,即可得出结果.
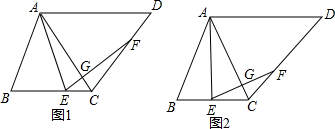
解答 解:(1)连接BD,如图1所示:
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)∵∠AOD=2∠ABD=120°,
∴$\widehat{AD}$的长=$\frac{120×π×2}{180}$=$\frac{4π}{3}$; (3)连接OA,如图2所示:
(3)连接OA,如图2所示:
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD-∠DOE=30°,
∴n=$\frac{360°}{30°}$=12.
点评 此题考查了圆的内接四边形的性质、圆周角定理以及等边三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如图是一个简单的数值运算程序,当输出y的值为-1时,则输入x的值为( )


| A. | 1 | B. | 5 | C. | -1 | D. | ±1 |
10.下列各组有理数的大小比较中,错误的是( )
| A. | -(-$\frac{1}{5}$)$<-\frac{1}{5}$ | B. | -(-3$\frac{2}{5}$)$>-3\frac{2}{5}$ | C. | -(+4)<+(+4) | D. | +(-1.1)<0 |
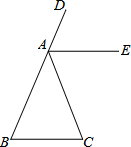 如图,已知∠DAC是△ABC的一个外角,请在下列三个关系:
如图,已知∠DAC是△ABC的一个外角,请在下列三个关系: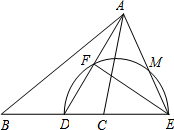 如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.
如图,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.