题目内容
 如图,在△ABC中,BM=MC,∠ABM=∠ACM.求证:点M在∠BAC的平分线上.
如图,在△ABC中,BM=MC,∠ABM=∠ACM.求证:点M在∠BAC的平分线上.考点:等腰三角形的判定与性质
专题:证明题
分析:过M作ME⊥AB于E,MF⊥AC于F,利用“AAS”证明△BME和△CMF全等,再根据全等三角形对应边相等可得ME=MF,再根据角平分线性质定理的逆定理从而得证.
解答: 证明:过M作ME⊥AB于E,MF⊥AC于F,
证明:过M作ME⊥AB于E,MF⊥AC于F,
在△BME和△CMF中,
,
∴△BME≌△CMF(AAS),
∴ME=MF,
∴点M在∠BAC的平分线上.
 证明:过M作ME⊥AB于E,MF⊥AC于F,
证明:过M作ME⊥AB于E,MF⊥AC于F,在△BME和△CMF中,
|
∴△BME≌△CMF(AAS),
∴ME=MF,
∴点M在∠BAC的平分线上.
点评:本题考查了三角形求得的判定和性质以及角平分线性质定理的逆定理,熟练掌握才能很好的解题.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
下列运算正确的是( )
| A、-0.2×(-1)=-0.2 |
| B、-1×(-1)=-1 |
| C、a÷(b+c)=a÷b+a÷c |
| D、m(a-b+c)=ma-mb+mc |
 如图,已知四边形ABCD中,∠ABC=120°,AD⊥BA,CD⊥BC,测得AB=30
如图,已知四边形ABCD中,∠ABC=120°,AD⊥BA,CD⊥BC,测得AB=30 在Rt△ABC中,DE垂直平分斜边AB于点D,且点E为AB的下方,DE=
在Rt△ABC中,DE垂直平分斜边AB于点D,且点E为AB的下方,DE= 如图,在△ABC中,∠BAC=90°.
如图,在△ABC中,∠BAC=90°.

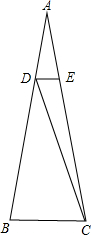 等腰△ABC中,AB=AC,∠A=20°,AD=BC,DE∥BC,求∠DCE的度数.
等腰△ABC中,AB=AC,∠A=20°,AD=BC,DE∥BC,求∠DCE的度数.