题目内容
如图,将弧BC 沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是 .


【解析】
试题分析:连接CA、CD;
根据折叠的性质,得: =
= ;
;
∴∠CAB=∠CBD+∠BCD;
∵∠CDA=∠CBD+∠BCD(三角形的一个外角等于和它不相邻的两个内角的和),
∴∠CAD=∠CDA,即△CAD是等腰三角形;
过C作CE⊥AB于E,则AE=DE=2.5;
∴BE=BD+DE=9.5;
在Rt△ACB中,CE⊥AB,根据射影定理,得:
BC2=BE•AB=9.5×12=114;
故BC= .
.

考点: 1.垂径定理;2. 圆周角定理;3.勾股定理;4.相似三角形的判定与性质

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 (0º<
(0º< ,小明掷B立方体朝上的数字为
,小明掷B立方体朝上的数字为 来确定点P(
来确定点P( ),那么它们各掷一次所确定 的点P落在已知直线
),那么它们各掷一次所确定 的点P落在已知直线 上的概率为 ( )
上的概率为 ( ) B.
B. C.
C. D.
D.
 与
与 轴相交于
轴相交于 、
、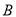 两点(点
两点(点 的左侧),与
的左侧),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.

 、
、 两点的坐标和抛物线的对称轴;
两点的坐标和抛物线的对称轴; ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点 ,点
,点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 作
作 交抛物线于点
交抛物线于点 ,设点
,设点 的横坐标为
的横坐标为 ;
;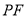 的长,并求出当
的长,并求出当 为平行四边形?
为平行四边形?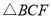 的面积为
的面积为 ,求
,求 与
与 的图象在
的图象在 轴上方的一部分,对于这段图象与
轴上方的一部分,对于这段图象与 轴所围成的阴影部分的面积,你认为与其最接近的值是( )
轴所围成的阴影部分的面积,你认为与其最接近的值是( )
 C.
C. D.32
D.32