��Ŀ����
��ͼ���ı���ABCO�Ǿ��Σ���A��3��0����B��3��4��������M��N�ֱ�ӵ�O��B��������ÿ��1����λ���ٶ��˶������е�M��OA���յ�A�˶�����N��BC���յ�C�˶�������N��NP��OC����AC�ڵ�P������MP����֪�����˶���x�룬��MPA�����ΪS��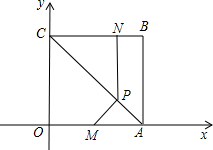
��1�����P�����꣮���ú�x�Ĵ���ʽ��ʾ��
��2��д��S����x�ĺ�����ϵʽ�������S�����ֵ��
��3������APM���ACO����ʱ�������P�����꣮
��4����PMA�ܷ��Ϊ���������Σ����ܣ�ֱ��д�����е�P�����ꣻ�粻�ܣ�˵�����ɣ�
��������1����ȷ��ֱ��AB�Ľ���ʽ���Լ�N�����������ȷ��P��ĺ����꣬�ٰ�������ֱ�߷��̽��P�����꣮
��2����P������������֪����MPA�б�AM�ϵĸߣ������AM�ij���������������������
��3������APM���ACO����ʱ��APM=90�㣬
=
����
=
���������ʽ���г�������ϵ�������x��ֵ���������P�����꣮
��4����PMA�ܳ�Ϊ����������ʱ�������߳���ȣ���ʱ�����������AM=AP����AP=PM����MP=MA�����ݹ��ɶ����ó�����x�ķ��̣�������̵Ľ⼴�ɣ�
��2����P������������֪����MPA�б�AM�ϵĸߣ������AM�ij���������������������
��3������APM���ACO����ʱ��APM=90�㣬
| AP |
| AM |
| AO |
| AC |
| AM |
| AP |
| AO |
| AC |
��4����PMA�ܳ�Ϊ����������ʱ�������߳���ȣ���ʱ�����������AM=AP����AP=PM����MP=MA�����ݹ��ɶ����ó�����x�ķ��̣�������̵Ľ⼴�ɣ�
����⣺��1����ֱ��AC�Ľ���ʽΪ��y=kx+b��
����A��3��0����C��0��4������ã�
y=-
x+4��
N��������3-x��4��������P���������3-x��
����ֱ�߽���ʽ��������Ϊ
x��
����P����������3-x��
x����
��2��AM���ϵĸ�ΪP�������꣬
������h=
x��
M��������x��0����
AM=3-x��
������S=
AM•h��
��ã�S=-
x2+2x=-
(x-
)2 +
��
���S�����ֵΪ
��
��3������Ŀ��֪AO=3��AC=5��AM=3-x��AP=
x��
��
=
��
=
����ã�
x=
����P��������
��
����
ͬ���ɵõ�
=
ʱ��
P��������
��2����
����P��������P1��
��
����P2��
��2����
��4����PMA�ܳ�Ϊ���������Σ�
�������������AM=APʱ��[3-��3-x��]2+(0-
x)2=��3-x��2��
��ã�x1=
��x2=-
����ȥ����
��3-x=
��
x=
��
��P�������ǣ�
��
����
��AP=PMʱ��[3-��3-x��]2+(0-
x)2=[��3-x��-x]2+(
x-0)2��
��ã�x1=1��x2=3����ȥ����
��3-x=2��
x=
��
��P�������ǣ�2��
����
��MP=MAʱ��[��3-x��-x]2+(
x-0)2=��3-x��2��
��ã�x1=0����ȥ����x2=
��
��3-x=
��
x=
��
��P�������ǣ�
��
����
��P�������ֱ�Ϊ
P1��2��
����P2��
��
����P3��
��
����
�𣺡�PMA�ܳ�Ϊ���������Σ���ʱP�������ֱ�Ϊ
P1��2��
����P2��
��
����P3��
��
����
����A��3��0����C��0��4������ã�
y=-
| 4 |
| 3 |
N��������3-x��4��������P���������3-x��
����ֱ�߽���ʽ��������Ϊ
| 4 |
| 3 |
����P����������3-x��
| 4 |
| 3 |
��2��AM���ϵĸ�ΪP�������꣬
������h=
| 4 |
| 3 |
M��������x��0����
AM=3-x��
������S=
| 1 |
| 2 |
��ã�S=-
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
���S�����ֵΪ
| 3 |
| 2 |
��3������Ŀ��֪AO=3��AC=5��AM=3-x��AP=
| 5 |
| 3 |
��
| AP |
| AM |
| AO |
| AC |
��
| ||
| 3-x |
| 3 |
| 5 |
x=
| 27 |
| 34 |
| 75 |
| 34 |
| 18 |
| 17 |
ͬ���ɵõ�
| AM |
| AP |
| AO |
| AC |
P��������
| 3 |
| 2 |
����P��������P1��
| 75 |
| 34 |
| 18 |
| 17 |
| 3 |
| 2 |
��4����PMA�ܳ�Ϊ���������Σ�
�������������AM=APʱ��[3-��3-x��]2+(0-
| 4 |
| 3 |
��ã�x1=
| 9 |
| 8 |
| 9 |
| 2 |
��3-x=
| 15 |
| 8 |
| 4 |
| 3 |
| 3 |
| 2 |
��P�������ǣ�
| 15 |
| 8 |
| 3 |
| 2 |
��AP=PMʱ��[3-��3-x��]2+(0-
| 4 |
| 3 |
| 4 |
| 3 |
��ã�x1=1��x2=3����ȥ����
��3-x=2��
| 4 |
| 3 |
| 4 |
| 3 |
��P�������ǣ�2��
| 2 |
| 3 |
��MP=MAʱ��[��3-x��-x]2+(
| 4 |
| 3 |
��ã�x1=0����ȥ����x2=
| 54 |
| 43 |
��3-x=
| 75 |
| 43 |
| 4 |
| 3 |
| 72 |
| 43 |
��P�������ǣ�
| 75 |
| 43 |
| 72 |
| 43 |
��P�������ֱ�Ϊ
P1��2��
| 4 |
| 3 |
| 15 |
| 8 |
| 3 |
| 2 |
| 75 |
| 43 |
| 72 |
| 43 |
�𣺡�PMA�ܳ�Ϊ���������Σ���ʱP�������ֱ�Ϊ
P1��2��
| 4 |
| 3 |
| 15 |
| 8 |
| 3 |
| 2 |
| 75 |
| 43 |
| 72 |
| 43 |
���������������ۺ��⣬��Ҫ�����˶��κ��������ʺ���ֵ��ͬʱ�������������ε����֪ʶ��

��ϰ��ϵ�д�
 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д�
�����Ŀ
 ����Aֹͣ��ͬʱһ����Q�ӵ�D��������ÿ��3����λ���ȵ��ٶ���DC���C�˶������Pͬʱֹͣ��
����Aֹͣ��ͬʱһ����Q�ӵ�D��������ÿ��3����λ���ȵ��ٶ���DC���C�˶������Pͬʱֹͣ��