Question

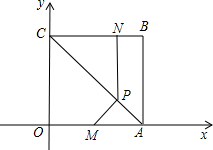
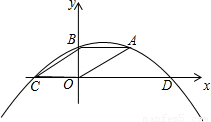
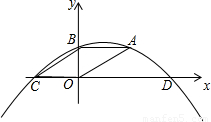
如图，四边形ABCO是平行四边形，AB=4，OB=2，抛物线过A、B、C三点，与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动，运动到A停止，同时一动点Q从点D出发，以每秒3个单位长度的速度沿DC向点C运动，与点P同时停止．
（1）求抛物线的解析式；
（2）若抛物线的对称轴与AB交于点E，与x轴交于点F，当点P运动时间t为何值时，四边形POQE是等腰梯形？
（3）当t为何值时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似？

Answer 1

分析：（1）根据AB、OB的长，即可得到A、B点的坐标；由于四边形ABCO是平行四边形，则AB=OC，由此可求出OC的长，即可得到C点的坐标，进而可用待定系数法求出抛物线的解析式；
（2）根据抛物线的解析式可求出D点的坐标及抛物线的对称轴方程，进而可求出E、F的坐标；若四边形POQE是等腰梯形，则OP=EQ，而OB=EF，可得BP=FQ，根据这个等量关系即可求出t的值；
（3）由于∠PBO、∠QOB都是直角，对应相等，若以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似，则有两种情况：
①P、Q在y轴同侧，②P、Q在y轴两侧；
每种情况又分为△PBO∽△QOB（此时两者全等），△PBO∽△BOQ两种情况；根据不同的相似三角形所得到的不同的比例线段即可求出t的值．

解答：解：（1）∵四边形ABCO是平行四边形，
∴OC=AB=4
∴A（4，2），B（0，2），C（-4，0）；（1分）
∵抛物线y=ax²+bx+c过点B，
∴c=2（2分）
由题意，有

16a-4b+2=0 16a+4b+2=2

解得

a=- 1 16 b= 1 4

（3分）
∴所求抛物线的解析式为y=-

1

16

x2+

1

4

x+2；（4分）

（2）将抛物线的解析式配方，得y=-

1

16

(x-2)2+2

1

4

∴抛物线的对称轴为x=2；（5分）
∴D（8，0），E（2，2），F（2，0）
欲使四边形POQE为等腰梯形，则有OP=QE，即BP=FQ；
∴t=6-3t，
即t=1.5；（7分）


（3）欲使以点P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似，
∵∠PBO=∠BOQ=90°，
∴有

BP

OB

=

OQ

BO

或

BP

OB

=

BO

OQ

，
即PB=OQ或OB²=PB•QO；
①若P、Q在y轴的同侧；
当PB=OQ时，t=8-3t，
∴t=2．（8分）
当OB²=PB•QO时，t（8-3t）=4，
即3t²-8t+4=0，
解得t=2，t=

2

3

；
②当P、Q在y轴的两侧；
当PB=OQ时，Q、C重合，P、A重合，此时t=4；
当OB²=PB•QO时，t（3t-8）=4，
即3t²-8t-4=0，
解得t=

4±2 7

3

；
∵t=

4-2 7

3

＜0，故舍去；
∴t=

4+2 7

3

；（11分）
∴当t=2或t=

2

3

，4或t=

4+2 7

3

秒时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似．（12分）

点评：此题是二次函数的综合类试题，涉及到二次函数解析式的确定、等腰梯形的判定、相似三角形的判定和性质等重要知识点，在求有关动点问题时要注意分析题意分情况讨论结果．