题目内容
如图，若O是△ABC内任意一点，点D，E，F分别在OA，OB，OC上，且DE∥AB，DF∥AC，AD：DO=1：2，
（1）求证：∠BAC=∠EDF；
（2）求EF：BC的值．
（1）求证：∠BAC=∠EDF；
（2）求EF：BC的值．
（1）∵DE∥AB，
∴∠BAD=∠EDO，
又∵DF∥AC，
∴∠CAD=∠FDO，
∴∠BAD+∠CAD=∠EDO+∠FDO，即∠BAC=∠EDF．
（2）∵AD：DO=1：2，
∴OD：OA=2：3，
∵DE∥AB，DF∥AC，
∴DE：AB=OD：OA=DF：AC，
∴
=
=
，
又∵∠BAC=∠EDF，
∴△FDE∽△CAB，
∴
=
=
．
∴∠BAD=∠EDO，
又∵DF∥AC，
∴∠CAD=∠FDO，
∴∠BAD+∠CAD=∠EDO+∠FDO，即∠BAC=∠EDF．
（2）∵AD：DO=1：2，
∴OD：OA=2：3，
∵DE∥AB，DF∥AC，
∴DE：AB=OD：OA=DF：AC，
∴
| DE |
| AB |
| DF |
| AC |
| 2 |
| 3 |
又∵∠BAC=∠EDF，
∴△FDE∽△CAB，
∴
| EF |
| BC |
| DE |
| AB |
| 2 |
| 3 |
练习册系列答案
相关题目
如图，若BD是△ABC的角平分线，则∠1=∠
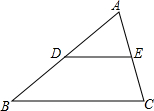如图，若DE是△ABC的中位线，△ABC的周长为1，则△ADE的周长为（ ）| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
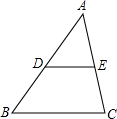如图，若DE是△ABC的中位线，△ABC的周长为6，则△ADE的周长为（ ）| A、4 | B、3 | C、2 | D、1 |
如图，若O是△ABC内任意一点，点D，E，F分别在OA，OB，OC上，且DE∥AB，DF∥AC，AD：DO=1：2，