题目内容
3.如图,△ABC中,AB=AC,AD∥BC,CD⊥AC,连BD,交AC于E.(1)如图1,若∠BAC=60°,求$\frac{AE}{BC}$的值;
(2)如图2,CF⊥AB于F,交BD于G,求证:CG=FG

分析 (1)先证明△ABC是等边三角形,得出AC=BC,∠ACB=60°,再证明∠ADC=30°,得出AD=2AC=2BC,由平行线的性质得出$\frac{AE}{CE}$=$\frac{AD}{BC}$=2,即可得出结果;
(2)作CQ∥AB于Q,则$\frac{CQ}{AB}=\frac{BC}{AD}$,$\frac{CG}{FG}=\frac{CQ}{BF}$,证明△CFB∽△DCA,得出对应边成比例$\frac{BF}{AC}$=$\frac{BC}{AD}$,得出$\frac{CQ}{AB}$=$\frac{BF}{AC}$,证出CQ=BF,即可得出结论.
解答 (1)解:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵AD∥BC,
∴∠DAC=∠ACB=60°,
∵CD⊥AC,
∴∠ACD=90°,
∴∠ADC=30°,
∴AD=2AC,
∴AD=2BC,
∵AD∥BC,
∴$\frac{AE}{CE}$=$\frac{AD}{BC}$=2,
∴$\frac{AE}{BC}=\frac{AE}{AC}$=$\frac{2}{3}$;
(2)证明:作CQ∥AB于Q,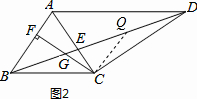
如图所示:则$\frac{CQ}{AB}=\frac{BC}{AD}$,$\frac{CG}{FG}=\frac{CQ}{BF}$,
∵AD∥BC,
∴$\frac{CE}{AE}=\frac{BC}{AD}$,∠ACB=∠DAC,
∴$\frac{CQ}{AB}=\frac{BC}{AD}$,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=∠DAC,
∵CF⊥AB,
∴∠BFC=90°=∠ACD,
∴△CFB∽△DCA,
∴$\frac{BF}{AC}=\frac{BC}{AD}$,
∴$\frac{CQ}{AB}=\frac{BF}{AC}$,
∴CQ=BF,
∴$\frac{CG}{FG}=\frac{CQ}{BF}$=1,
∴CG=FG.
点评 本题考查了等边三角形的判定与性质、相似三角形的判定与性质、等边三角形的性质、正确的作出辅助线是解题的关键.

| A. | i=cosα | B. | i=sinα | C. | i=cotα | D. | i=tanα |
| A. | 120πcm2 | B. | 60πcm2 | C. | 160πcm2 | D. | 80πcm2 |
 如图,AC∥BD,∠C=90°,∠ABC=∠EDB,AC=BE,求证;△ABC≌△EDB.
如图,AC∥BD,∠C=90°,∠ABC=∠EDB,AC=BE,求证;△ABC≌△EDB.