题目内容
若关于x的一元二次方程x2+px+q=0的两根分别5-
和5+
,则p= ,q= .
| 3 |
| 3 |
考点:根与系数的关系
专题:
分析:根据根与系数的关系得到(5-
)+(5+
)=-p,(5-
)•(5+
)=q,然后进行二次根式的运算可求出p与q的值.
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:根据题意得(5-
)+(5+
)=-p,(5-
)•(5+
)=q,
所以p=-10,q=22.
故答案为-10,22.
| 3 |
| 3 |
| 3 |
| 3 |
所以p=-10,q=22.
故答案为-10,22.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
无论m取何值,下列各式都有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x1,x2是一元二次方程x2-2x-1=0的两根,则x12+x22的值是( )
| A、6 | B、2 | C、-2 | D、4 |
解方程:
(1)x2-4x-3=0;
(2)(x-3)2+2x(x-3)=0;
(3)2x2-10x=3;
(4)(x-5)(x+2)=8;
(5)3x2+5(2x+1)=0;
(6)2x2-7x-4=0.
(1)x2-4x-3=0;
(2)(x-3)2+2x(x-3)=0;
(3)2x2-10x=3;
(4)(x-5)(x+2)=8;
(5)3x2+5(2x+1)=0;
(6)2x2-7x-4=0.
下列一元二次方程中,两实数根的和等于-4的是( )
| A、x2+2x-4=0 |
| B、x2-2x+4=0 |
| C、x2-4x-5=0 |
| D、x2+4x-5=0 |
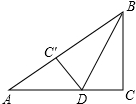 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )