题目内容
13. 某企业生产并销售某种产品,假设销售量与产量相等,图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段CD所表示的y2与x之间的函数表达式;
(3)当该产品产量为90kg时,获得的利润是多少?
分析 (1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)根据线段线段CD经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(3)先将x=90代入(2)中所求的解析式,求出y2的值,再根据利润=每千克利润×产量列式即可求解.
解答 解:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)设y2与x之间的函数关系式为y2=kx+b,
∵经过点(0,120)与(130,42),
∴$\left\{\begin{array}{l}{b=120}\\{130k+b=42}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-0.6}\\{b=120}\end{array}\right.$,
∴线段CD所表示的一次函数的表达式为y2=-0.6x+120(0≤x≤130);
(3)将x=90代入y2=-0.6x+120,得y2=-0.6×90+120=66,
所以利润为(66-42)×90=2160(元).
答:当该产品产量为90kg时,获得的利润是2160元.
点评 本题主要考查一次函数的应用,待定系数法求一次函数的表达式,解题的关键是从实际问题中抽象出一次函数模型,难度不大.

练习册系列答案
相关题目
3. 如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
 如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
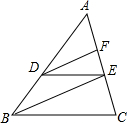 如图,在△ABC中,D是AB 上一点,且$\frac{AD}{DB}$=$\frac{3}{2}$,E、F是AC上的点,且DE∥BC,DF∥BE,AF=9.求EC的长.
如图,在△ABC中,D是AB 上一点,且$\frac{AD}{DB}$=$\frac{3}{2}$,E、F是AC上的点,且DE∥BC,DF∥BE,AF=9.求EC的长.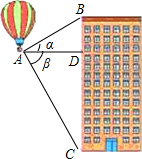 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC.
如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC. 已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.
已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.