题目内容
9.已知点A(2,4),B(4,a),C(b,-$\frac{8}{3}$)都在反比例函数y=$\frac{k}{x}$的图象上.(1)分别求出k,a和b的值.
(2)若P,Q,R是该反比例函数图象上的三点,分别过P,Q,R三点向x轴、y轴作垂线,构成三个矩形,他们的面积分别是S1,S2,S3,试比较S1,S2,S3的大小.
(3)若H是该函数图象上一点,延长HO交该函数的图象于点M,HN⊥x轴,MN⊥y轴,HN与MN交于点N,求△HMN的面积.
分析 (1)根据反比例函数图象上点的坐标特征,求得k的值,然后将点B、C的坐标分别代入该反比例函数的解析式,列出关于a、b的二元一次方程组,通过解方程组即可求得.
(2)根据过双曲线上任意一点引x轴、y轴垂线,所得矩形面积S是个定值,即S=|k|,判断S1=S2=S3.
(3)此题可根据反比例函数的对称性得H、M两点关于原点对称,再由反比例函数系数k的几何意义可得出△HMN的面积.
解答 解:(1)∵点A(2,4)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=2×4=8,
∵B(4,a),C(b,-$\frac{8}{3}$)都在反比例函数y=$\frac{8}{x}$的图象上
∴$\left\{\begin{array}{l}{a=\frac{8}{4}}\\{-\frac{8}{3}=\frac{8}{b}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$.
(2)设点P坐标为(x1,y1) 点Q坐标(x2,y2) 点R坐标(x3,y3),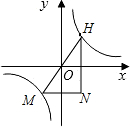
∵S1=x1•y1=k,S2=x2•y2=k,S3=x3•y3=k,
∴S1=S2=S3.
(3)如图,设点H的坐标为(x,y),则点M坐标为(-x,-y),
所以HN=2y,MN=2x,
所以Rt△HMN的面积为$\frac{1}{2}$MN•HN=$\frac{1}{2}$×2x•2y=2xy=2|k|=16.
点评 本题主要考查反比例函数图象上点的坐标特征和比例函数y=$\frac{k}{x}$中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
14.若a-b=2,则a2-b2-4b的值是( )
| A. | 2 | B. | 0 | C. | 4 | D. | 6 |
18.下列各式不能用平方差公式的是( )
| A. | (x+y)(x-y) | B. | (x+2y)(2x-y) | C. | (x3+y3)(x3-y3) | D. | (-x-y)(x-y) |
19.代数式a3b2-$\frac{1}{2}$a2b3,$\frac{1}{2}$a3b4+a4b3,a4b2-a2b4的公因式是( )
| A. | a3b2 | B. | a2b2 | C. | a2b3 | D. | a2b4 |
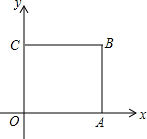 如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.
如图,在平面直角坐标系中,正方形OABC的一个顶点为B(1,1),点A,C分别在x轴,y轴上.