题目内容
4.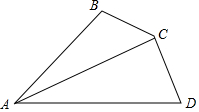 如图,四边形ABCD中,AC平分∠BAD,∠B+∠D=180°,求证:BC=CD.
如图,四边形ABCD中,AC平分∠BAD,∠B+∠D=180°,求证:BC=CD.
分析 过点C作CE⊥AB交AB的延长线于E,作CF⊥AD于F,根据角平分线上的点到角的两边距离相等可得CE=CF,根据同角的补角相等求出∠D=∠CBE,然后利用“角角边”证明△BCE和△DCF全等,根据全等三角形对应边相等证明即可.
解答 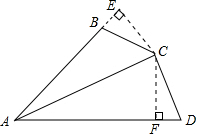 证明:如图,过点C作CE⊥AB交AB的延长线于E,作CF⊥AD于F,
证明:如图,过点C作CE⊥AB交AB的延长线于E,作CF⊥AD于F,
∵AC平分∠BAD,
∴CE=CF,
∵∠ABC+∠CBE=180°,∠ABC+∠D=180°,
∴∠D=∠CBE,
在△BCE和△DCF中,$\left\{\begin{array}{l}{∠D=∠CBE}\\{∠E=∠CFD=90°}\\{CE=CF}\end{array}\right.$,
∴△BCE≌△DCF(AAS),
∴BC=CD.
点评 本题考查了全等三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟记性质以及三角形全等的判定方法是解题的关键.

练习册系列答案
相关题目
12.某玻璃制品销售公司职工的月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售件数),如表是甲、乙两位职工某月的工资情况.
(1)求职工的月基本保障工资和销售每件产品的奖励金额各是多少元?
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
| 职工 | 甲 | 乙 |
| 月销售件数(件) | 200 | 180 |
| 月工资(元) | 1800 | 1700 |
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
14.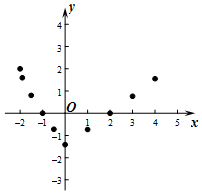 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
小军根据学习函数的经验,对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2;
(2)表是y与x的几组对应值?
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察图象,函数的最小值是-$\sqrt{2}$;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外):当-2≤x<0时,y随x的增大而减小.
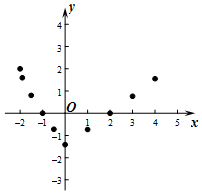 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?小军根据学习函数的经验,对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2;
(2)表是y与x的几组对应值?
| x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
| y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
(3)观察图象,函数的最小值是-$\sqrt{2}$;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外):当-2≤x<0时,y随x的增大而减小.