题目内容
 已知抛物线y=
已知抛物线y=| 1 | 2 |
(1)求:k的取值范围;
(2)设抛物线与x轴交于A、B两点,且点A(-1,0)在点B的左侧,点D是抛物线的顶点,试判断△ABD是不是等腰直角三角形?并说明理由;
(3)在(2)的条件下,抛物线与y轴交于点C,点E在y轴的正半轴上,且以A、O、E为顶点的三角形和以B、O、C为顶点的三角形相似,求:点E的坐标.
分析:(1)根据抛物线与x轴有两个交点,△≥0列出不等式求解即可;
(2)把点A坐标代入抛物线求出k值,再求出点B、D的坐标,设抛物线对称轴与x轴交点为F,求出AF=BF=DF,从而求出∠ADF=∠DAF=∠BDF=∠DBF=45°,即可得到△ABD是等腰直角三角形;
(3)分OA和OB是对应边,OA和OC是对应边两种情况,根据相似三角形对应边成比例列式求出OE的长度,再根据点E在y轴正半轴写出坐标即可.
(2)把点A坐标代入抛物线求出k值,再求出点B、D的坐标,设抛物线对称轴与x轴交点为F,求出AF=BF=DF,从而求出∠ADF=∠DAF=∠BDF=∠DBF=45°,即可得到△ABD是等腰直角三角形;
(3)分OA和OB是对应边,OA和OC是对应边两种情况,根据相似三角形对应边成比例列式求出OE的长度,再根据点E在y轴正半轴写出坐标即可.
解答:解:(1)∵抛物线y=
x2-x+k与x轴有两个交点,
∴△=b2-4ac=(-1)2-4×
k>0,
解得k<
;
(2)△ABD是等腰直角三角形.
理由如下:将点A(-1,0)代入抛物线y=
x2-x+k得,
×(-1)2-(-1)+k=0,
解得k=-
,
∴y=
x2-x-
,
令y=0,则
x2-x-
=0,
整理得,x2-2x-3=0,
解得x1=-1,x2=3,
∴点B(3,0),
∵y=
x2-x-
=
(x-1)2-2,
∴点D(1,-2),
设抛物线对称轴与x轴交点为F,
则AF=BF=DF=2,
∴∠ADF=∠DAF=∠BDF=∠DBF=45°,
∴△ABD是等腰直角三角形;
(3)∵(3,0),C(0,-
),
∴OB=3,OC=
,
OA和OB是对应边时,△BOC∽△AOE,
∴
=
,
即
=
,
解得OE=
,
此处,点E1(0,
),
OA和OC是对应边时,△BOC∽△EOA,
∴
=
,
即
=
,
解得OE=2,
此时,点E2(0,2),
综上所述,点E的坐标为(0,
)或(0,2)时,以A、O、E为顶点的三角形和以B、O、C为顶点的三角形相似.
| 1 |
| 2 |
∴△=b2-4ac=(-1)2-4×
| 1 |
| 2 |
解得k<
| 1 |
| 2 |
(2)△ABD是等腰直角三角形.
理由如下:将点A(-1,0)代入抛物线y=
| 1 |
| 2 |
| 1 |
| 2 |
解得k=-
| 3 |
| 2 |
∴y=
| 1 |
| 2 |
| 3 |
| 2 |
令y=0,则
| 1 |
| 2 |
| 3 |
| 2 |
整理得,x2-2x-3=0,

解得x1=-1,x2=3,
∴点B(3,0),
∵y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴点D(1,-2),
设抛物线对称轴与x轴交点为F,
则AF=BF=DF=2,
∴∠ADF=∠DAF=∠BDF=∠DBF=45°,
∴△ABD是等腰直角三角形;
(3)∵(3,0),C(0,-
| 3 |
| 2 |
∴OB=3,OC=
| 3 |
| 2 |
OA和OB是对应边时,△BOC∽△AOE,
∴
| OA |
| OB |
| OE |
| OC |
即
| 1 |
| 3 |
| OE | ||
|
解得OE=
| 1 |
| 2 |
此处,点E1(0,
| 1 |
| 2 |
OA和OC是对应边时,△BOC∽△EOA,
∴
| OA |
| OC |
| OE |
| OB |
即
| 1 | ||
|
| OE |
| 3 |
解得OE=2,
此时,点E2(0,2),
综上所述,点E的坐标为(0,
| 1 |
| 2 |
点评:本题是二次函数综合题型,主要利用了抛物线与x轴的交点问题,等腰直角三角形的判定,相似三角形的判定与性质,难点在于(3)要分情况讨论.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
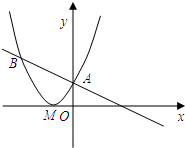 角形?若存在,求出点P的坐标;若不存在,请说明理由.
角形?若存在,求出点P的坐标;若不存在,请说明理由.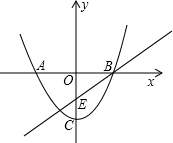 已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=
已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=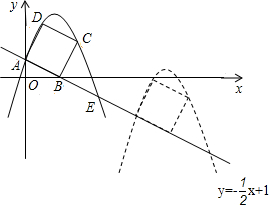
 如图,已知直线
如图,已知直线 +12x-19的顶点的横坐标是3,则a=________.
+12x-19的顶点的横坐标是3,则a=________.