题目内容
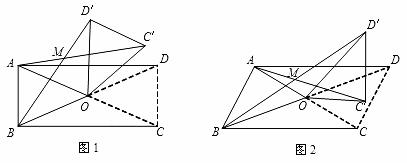
在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB =α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
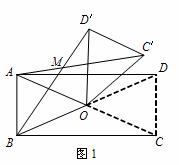
(1)当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
(1)证明:在矩形ABCD中,
∵AC=BD,OA=OC=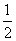 AC,OB=OD=
AC,OB=OD=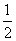 BD,
BD,
∴OA=OC=OB=OD,
∵△D′OC′由△DOC旋转得到,
∴OD=OD′,OC=OC′,∠D′OD=∠C′OC,
∴OB=OD′=OA=OC′,…………1分
∴180°-∠D′OD=180°-∠C′OC,
即∠BOD′=∠AOC′,…………2分
∴△BOD′≌△AOC′…………3分
(2)①猜想:△BOD′∽△AOC′.
证明:在平行四边形ABCD中,OB=OD,OA=OC,
∵△D′OC′由△DOC旋转得到,
∴OD=OD′,OC=OC′,∠D′OD=∠C′OC,
∴OB:OA=OD′:OC′,…………4分
180°-∠D′OD=180°-∠C′OC,
∴∠BOD′=∠AOC′,…………5分
∴△BOD′∽△AOC′…………6分
②结论:AC′=kBD′,∠AMB=α
证明:∵△BOD′∽△AOC′,
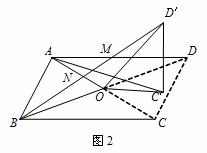
∴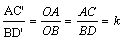 ,即AC′=kBD′ …………7分
,即AC′=kBD′ …………7分
设BD′与AC相交于点N,∵△BOD′∽△AOC′,∴∠OBM=∠OAM,
在△ANM与△BNO中,又∵∠ANM=∠BNO,
∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO,
即∠AMB=∠AOB=α.………………9分

二次函数y=ax2+bx+c(a≠0)的部分对应值如下表:
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
则二次函数y=ax2+bx+c在x=2时,y=___________.
 ,求⊙O的半径.
,求⊙O的半径.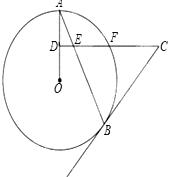
 AB的交点
AB的交点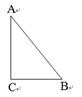
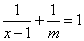 的解为………………………………………………………………………………………【 】
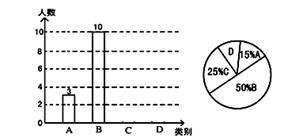
的解为………………………………………………………………………………………【 】 学生的自主学习、合作交流能力有了很大提高.九(2)班的陈老师为了解本班学生自主学习、合作交流的具体情况,对部分同学进行了一段时间的跟踪调查,将调查结果(分为A:特别好;B:好;C:一般;D:较差四类)绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
学生的自主学习、合作交流能力有了很大提高.九(2)班的陈老师为了解本班学生自主学习、合作交流的具体情况,对部分同学进行了一段时间的跟踪调查,将调查结果(分为A:特别好;B:好;C:一般;D:较差四类)绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: