Question

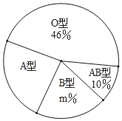
【题目】“只要人人献出一点爱，世界将变成美好的人间”．某大学利用“世界献血日”开展自愿义务献血活动，经过检测，献血者血型有“A、B、AB、O”四种类型，随机抽取部分献血结果进行统计，根据结果制作了如图两幅不完整统计图表（表，图）：

血型统计表

血型	A	B	AB	O
人数		10	5

（1）本次随机抽取献血者人数为　 　人，图中m＝　 　；

（2）补全表中的数据；

（3）若这次活动中该校有1300人义务献血，估计大约有多少人是A型血？

（4）现有4个自愿献血者，2人为O型，1人为A型，1人为B型，若在4人中随机挑选2人，利用树状图或列表法求两人血型均为O型的概率．

Answer 1

【答案】（1）50,20；（2）12,23；（3）312；（4）.

【解析】

（1）用AB型的人数除以它所占的百分比得到随机抽取的献血者的总人数，然后计算m的值；

（2）先计算出O型的人数，再计算出A型人数，从而可补全上表中的数据；

（3）用样本中A型的人数除以50得到血型是A型的概率，然后用3000乘以此概率可估计这3000人中是A型血的人数；

（4）画出树状图，根据概率公式即可得到结果．

解：（1）这次随机抽取的献血者人数为5÷10%＝50（人），

所以m＝×100＝20；

故答案为50，20；

（2）O型献血的人数为46%×50＝23（人），

A型献血的人数为50﹣10﹣5﹣23＝12（人），

血型	A	B	AB	O
人数	12	10	5	23

故答案为12，23；

（3）从献血者人群中任抽取一人，其血型是A型的概率＝＝，1300×＝312，估计这1300人中大约有312人是A型血；

（4）画树状图如图所示，

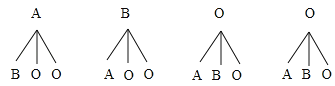
所以P（两个O型）＝＝．