题目内容
【题目】已知二次函数
．
（1）求出该函数图象的顶点坐标，对称轴，图象与
轴、
轴的交点坐标；
（2）在什么范围内时，随的增大而增大？当在什么范围内时，随的增大而减小？
（3）当在什么范围内时，
？
【答案】（1）：
；（2）当
时，
随
的增大而增大；当
时，随的增大而减小；（3）当
时，
．
【解析】
（1）把抛物线化成顶点式的形式，即可写出顶点坐标，对称轴，再当y=0时：-
x2+
x+2=0，计算出x的值，可得到与x轴的交点坐标，当x=0，计算出y=2，可得到与y轴的交点坐标；
（2）（3）由（1）中所求的数值画出二次函数图象，根据图象可以直观的得到答案．
（1）
，
对称轴是
，
顶点坐标是
，
当
时：
，
解得：
，
，
∴与轴的交点坐标是：
，
当
时：
，
∴与轴的交点坐标是：；
（2）画图象可知：当时，随的增大而增大，
当时，随的增大而减小；
（3）由图象可知：当时，．
练习册系列答案
相关题目
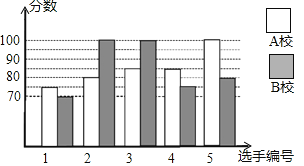
【题目】某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．
根据图示填写下表：
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；
计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．
