题目内容
 27、如图⊙O的内接△ABC中,外角∠ACF的角平分线与⊙O相交于D点,DP⊥AC,垂足为P,DH⊥BF,垂足为H.问:
27、如图⊙O的内接△ABC中,外角∠ACF的角平分线与⊙O相交于D点,DP⊥AC,垂足为P,DH⊥BF,垂足为H.问:(1)∠PDC与∠HDC是否相等,为什么?
(2)图中有哪几组相等的线段?
(3)当△ABC满足什么条件时,△CPD∽△CBA,为什么?
分析:(1)根据角平分线与垂线的性质证明角相等;
(2)发现全等三角形,根据全等三角形的对应边相等证明出线段相等;
(3)根据其中一个是直角三角形得到AC必须是直径.再根据另一对角对应相等,结合利用平角发现必须都是60°才可.
(2)发现全等三角形,根据全等三角形的对应边相等证明出线段相等;
(3)根据其中一个是直角三角形得到AC必须是直径.再根据另一对角对应相等,结合利用平角发现必须都是60°才可.
解答:解:(1)答:相等.
∵CD为∠ACF的角平分线(已知),
∴∠DCP=∠DCH,DP⊥AC,DH⊥BF.
∴∠DPC=∠DHC=90°.
∴∠PDC=∠HDC.
(2)PC=HC,DP=DH,AP=BH,AD=BD.
(3)∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
∵∠CPD=90°,
∴∠ABC=90°.
∵CD为∠ACF的角平分线,∠PCD=∠DCF=∠ACB,
∴∠ACB=60°.
∴∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
∵CD为∠ACF的角平分线(已知),
∴∠DCP=∠DCH,DP⊥AC,DH⊥BF.
∴∠DPC=∠DHC=90°.
∴∠PDC=∠HDC.
(2)PC=HC,DP=DH,AP=BH,AD=BD.
(3)∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
∵∠CPD=90°,
∴∠ABC=90°.
∵CD为∠ACF的角平分线,∠PCD=∠DCF=∠ACB,
∴∠ACB=60°.
∴∠ABC=90°且∠ACB=60°时,△CPD∽△CBA.
点评:掌握全等三角形的判定和性质,能够根据已知的三角形的形状探索若相似应满足的条件.

练习册系列答案
相关题目
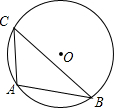 如图△ABC的内接圆于⊙O,∠C=45°,AB=4,则⊙O的半径为( )
如图△ABC的内接圆于⊙O,∠C=45°,AB=4,则⊙O的半径为( )A、2
| ||
| B、4 | ||
C、2
| ||
| D、5 |
如图△ABC的内接圆于⊙O,∠C=45°,AB=4,则⊙O 的半径为( )
A. | B.4 | C. | D.5 |

 B.4 C.
B.4 C. D.5
D.5 如图△ABC的内接圆于⊙O,∠C=45°,AB=4,则⊙O的半径为( )
如图△ABC的内接圆于⊙O,∠C=45°,AB=4,则⊙O的半径为( )



