Question

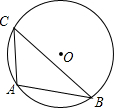如图△ABC的内接圆于⊙O，∠C=45°，AB=4，则⊙O的半径为（　　）

• A、2

  2

• B、4
• C、2

  3

• D、5

Answer 1

分析：可连接OA、OB，根据圆周角定理，易知：∠AOB=90°，即△AOB是等腰直角三角形；已知了斜边AB的长，可求出直角边即半径的长．

解答：解：如图，连接OA、OB，
由圆周角定理知，∠AOB=2∠C=90°；
∵OA=OB，
∴△AOB是等腰直角三角形；
则OA=AB•sin45°=4×

2

2

=2

2

．
故选A．

点评：本题主要考查了等腰直角三角形的性质和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．