Question

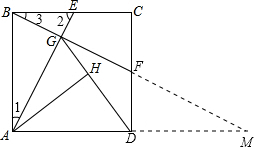
正方形ABCD中，E点为BC中点，连接AE，过B点作BF⊥AE，交CD于F点，交AE于G点，连接GD，过A点作AH⊥GD交GD于H点．
（1）求证：△ABE≌△BCF；
（2）若正方形边长为4，AH=

16

5

，求△AGD的面积．

Answer 1

分析：（1）易得∠1=∠3，这两个三角形中都有一个角是直角，加上正方形的边长相等，利用角边角可得这两个三角形全等；
（2）求得DG的长就可以求得△AGD的面积．易得F为CD的中点，延长BF交AD的延长线于点M，可构造出△BCF≌△MDF，那么可得DM=BC=AD，就可以求得GD的长，也就求得了△AGD的面积．

解答：证明：（1）正方形ABCD中，∠ABE=90°，

∴∠1+∠2=90°，
又AE⊥BF，
∴∠3+∠2=90°，
则∠1=∠3             
又∵四边形ABCD为正方形，
∴∠ABE=∠BCF=90°，AB=BC
在△ABE和△BCF中，

∠1=∠3 AB=BC ∠ABE=∠BCF

∴△ABE≌△BCF（ASA）         

（2）延长BF交AD延长线于M点，
∴∠MDF=90°             
由（1）知△ABE≌△BCF，
∴CF=BE
∵E点是BC中点，
∴BE=

1

2

BC，即CF=

1

2

CD=FD，
在△BCF和△MDF中，

∠BCF=∠MDF CF=DF ∠BFC=∠MFD

∴△BCF≌△MDF（ASA）
∴BC=DM，即DM=AD，D是AM中点                         
又AG⊥GM，即△AGM为直角三角形，
∴GD=

1

2

AM=AD
又∵正方形边长为4，
∴GD=4
S_△AGD=

1

2

GD•AH=

1

2

×4×

16

5

=

32

5

．

点评：综合考查了正方形的性质与全等三角形的判定与性质；利用正方形一边的中点构造全等三角形是常用的辅助线方法，是解决本题的难点．