题目内容
7. 如图,抛物线y=ax2+bx+c经过A(-1,0)、B(4,0)、C(0,-2)三点.
如图,抛物线y=ax2+bx+c经过A(-1,0)、B(4,0)、C(0,-2)三点.(1)求抛物线的函数关系式;
(2)若直线l是抛物线的对称轴,设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在线段AB上是否存在点M(m,0),使得以线段CM为直径的圆与边BC交于Q点(与点C不同),且以点Q、B、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
分析 (1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可.
(2)由图知:A、B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知:若连接BC,那么BC与直线l的交点即为符合条件的P点.
(3)由于△QBO的腰和底没有明确,因此要分三种情况来讨论:①QB=BO、②QB=QO、③QO=BO;可先设出M点的坐标,然后用M点纵坐标表示△QBO的三边长,再按上面的三种情况列式求解即可.
解答 解:∵y=ax2+bx+c经过A(-1,0)、B(4,0)、C(0,-2),
∴$\left\{\begin{array}{l}{16a+4b+c=0}\\{a-b+c=0}\\{c=-2}\end{array}\right.$,
解之得$\left\{\begin{array}{l}a=\frac{1}{2}\\ b=-\frac{3}{2}\\ c=-2\end{array}\right.$,
∴函数解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2;
(2)如图1,抛物线的对称轴是直线x=1.5.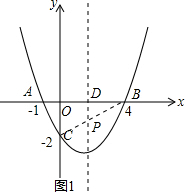
当点P落在线段BC上时,PA+PC最小,△PAC的周长最小.
设抛物线的对称轴与x轴的交点为D.
∵B(4,0)、C(0,-2).
∴OB=4,OC=2.
又OD=$\frac{3}{2}$,得BD=$\frac{5}{2}$.
由$\frac{BD}{BO}=\frac{PD}{OC}$,得
PD=$\frac{5}{4}$.
∴点P的坐标为($\frac{3}{2}$,$-\frac{5}{4}$).
(3)过点Q作QM⊥BC交AB于点M,如图2,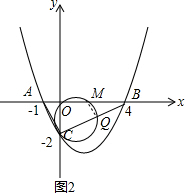
则根据直径所对圆周角是直角的性质,知点Q在以CM为直径的圆上,
由A(-1,0)、B(4,0)、C(0,-2)可证△ABC是直角三角形,得∠ACB=90°,
∴QM∥AC,
∴△BMQ∽△BAC.
∴$\frac{BQ}{BC}=\frac{BM}{AB}$,
由A(-1,0)、B(4,0)、C(0,-2),可得OA=1,OB=4,OC=2.
则AB=1+4=5,BC=$\sqrt{{2^2}+{4^2}}=2\sqrt{5}$.
由M(m,0),得BM=4-m.
分三种情况:
①当QB=QO时,点Q在OB垂直平分线上,是BC的中点,得QC=$\sqrt{5}$.
∴$\frac{{\sqrt{5}}}{{2\sqrt{5}}}=\frac{4-m}{5}$,解得$m=\frac{3}{2}$.
②当BQ=BO时,BQ=4.
∴$\frac{4}{{2\sqrt{5}}}=\frac{4-m}{5}$,解得$m=4-2\sqrt{5}$.
③当OB=OQ时,由于OQ=4,OA=2,OQ>OA从而点Q在CB的延长线上,这样点M不在线段AC上.
综上所述,m的值为$\frac{3}{2}$或$4-2\sqrt{5}$.
点评 该二次函数综合题涉及了抛物线的性质及解析式的确定、等腰三角形的判定等知识,在判定等腰三角形时,一定要根据不同的腰和底分类进行讨论,以免漏解.

| A. | 赚24元 | B. | 赔24元 | C. | 不赚不赔 | D. | 无法确定 |
| 区县 | 成华 | 武侯 | 青羊 | 金牛 | 锦江 | 高新 | 龙泉 | 新都 | 双流 |
| 最高气温 | 32 | 33 | 30 | 31 | 30 | 32 | 32 | 29 | 30 |
| A. | 30 | B. | 30.5 | C. | 31 | D. | 32 |
 某校七年级(一)班共有50名学生,分别参加了写作、数学、英语、篮球及摄影兴趣小组,每个学生必须参加且只能参加其中一种,请根据如图所示的扇形统计图.求:
某校七年级(一)班共有50名学生,分别参加了写作、数学、英语、篮球及摄影兴趣小组,每个学生必须参加且只能参加其中一种,请根据如图所示的扇形统计图.求: 如图所示,在平面直角坐标系xOy中,A(-1,5),B(-1,0),
如图所示,在平面直角坐标系xOy中,A(-1,5),B(-1,0), 如图,△ABC中,点D在边BC上,且∠BAD=90°,BD=2AC,∠B=25°,则∠C度数是50°.
如图,△ABC中,点D在边BC上,且∠BAD=90°,BD=2AC,∠B=25°,则∠C度数是50°.