题目内容
 如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标.
(3)求△A′B′C′的面积.
考点:作图-平移变换
专题:
分析:(1)根据△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)可知△ABC应向右平移6个单位,向上平移4个单位,由此作出△A′B′C′即可;
(2)根据各点在坐标系中的位置写出点A′、B′、C′的坐标即可;
(3)根据△A′B′C′的面积等于长方形的面积减去三个角上三角形的面积即可.
(2)根据各点在坐标系中的位置写出点A′、B′、C′的坐标即可;
(3)根据△A′B′C′的面积等于长方形的面积减去三个角上三角形的面积即可.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)由图可知,A′(2,3)、B′(1,0)、C′(5,1);
(3)S△A′B′C′=3×4-
×1×3-
×1×4-
×2×3
=12-
-2-3
=
.
 解:(1)如图所示;
解:(1)如图所示;(2)由图可知,A′(2,3)、B′(1,0)、C′(5,1);
(3)S△A′B′C′=3×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=12-
| 3 |
| 2 |
=
| 11 |
| 2 |
点评:本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
下列说法:[1]两个菱形一定相似;[2]两个等边三角形一定相似;[3]两个正方形一定相似;[4]两个矩形一定相似;[5]两个全等三角形一定相似;[6]两个直角三角形一定相似.其中正确的有( )个.
| A、1 | B、2 | C、3 | D、4 |
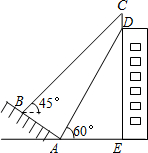 如图,某校一幢教学大楼的顶部竖有一块宣传牌CD=2米.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
如图,某校一幢教学大楼的顶部竖有一块宣传牌CD=2米.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1: