题目内容
 如图,∠A是⊙O的圆周角,∠OBC=30°,则∠A的度数为________度.
如图,∠A是⊙O的圆周角,∠OBC=30°,则∠A的度数为________度.
60
分析:由OB=OC可得到∠OBC=∠OCB=30°,则∠BOC=180°-30°-30°=120°,然后根据圆周角定理得到∠A= ∠BOC=60°.
∠BOC=60°.
解答:∵∠A是⊙O的圆周角,
∴∠A= ∠BOC,
∠BOC,
∵∠OBC=30°,OB=OC,
∴∠BOC=180°-30°-30°=120°,
∴∠A= ×120°=60°.
×120°=60°.
故答案为60.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.
分析:由OB=OC可得到∠OBC=∠OCB=30°,则∠BOC=180°-30°-30°=120°,然后根据圆周角定理得到∠A=
 ∠BOC=60°.
∠BOC=60°.解答:∵∠A是⊙O的圆周角,
∴∠A=
 ∠BOC,
∠BOC,∵∠OBC=30°,OB=OC,
∴∠BOC=180°-30°-30°=120°,
∴∠A=
 ×120°=60°.
×120°=60°.故答案为60.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是
(1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是
 如图,半径是5厘米的圆中,8厘米长的弦的弦心距是________厘米.
如图,半径是5厘米的圆中,8厘米长的弦的弦心距是________厘米.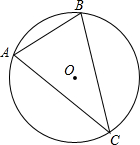 如图,⊙O是△ABC的________圆,△ABC是⊙O的________三角形.
如图,⊙O是△ABC的________圆,△ABC是⊙O的________三角形. 如图,半径是5厘米的圆中,8厘米长的弦的弦心距是 厘米.
如图,半径是5厘米的圆中,8厘米长的弦的弦心距是 厘米.