题目内容
7.计算:$\frac{2{x}^{2}+3x-2}{2{x}^{3}+{x}^{2}-3x-2}$-$\frac{{x}^{2}-1}{{x}^{3}+x-2}$=$\frac{1}{{x}^{2}+x+2}$.分析 把被减数与减数约分后,再进行加减.
解答 ∵$\frac{2{x}^{2}+3x-2}{2{x}^{3}+{x}^{2}+3x-2}$
=$\frac{(2x-1)(x+2)}{(2{x}^{3}-{x}^{2})+(2{x}^{2}+3x-2)}$
=$\frac{(2x-1)(x+2)}{{x}^{2}(2x-1)+(2x-1)(x+2)}$
=$\frac{(2x-1)(x+2)}{(2x-1)({x}^{2}+x+2)}=\frac{x+2}{{x}^{2}+x+2}$
又∵$\frac{{x}^{2}-1}{{x}^{3}+x-2}=\frac{(x+1)(x-1)}{({x}^{3}-1)+(x-1)}$
=$\frac{(x+1)(x-1)}{(x-1)({x}^{2}+x+2)}=\frac{x+1}{{x}^{2}+x+2}$
∴原式=$\frac{x+2}{{x}^{2}+x+2}-\frac{x+1}{{x}^{2}+x+2}=\frac{1}{{x}^{2}+x+2}$
点评 本题考查了分式的加减、多项式的因式分解.被减数和减数的分式约分是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的角平分线BO、CO交于O点,过O点作DE∥BC,求出∠BOC的大小.
如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的角平分线BO、CO交于O点,过O点作DE∥BC,求出∠BOC的大小. 星晴天,小亮从家里骑自行车到同学家去玩,然后返回,如图是他离家的路程y(千米)与实际x(分钟)的函数图象,下列说法:
星晴天,小亮从家里骑自行车到同学家去玩,然后返回,如图是他离家的路程y(千米)与实际x(分钟)的函数图象,下列说法: 如图,AB∥CD,∠B=120°,EF是∠CEB的平分线,FG∥HD,求∠EDH的度数.
如图,AB∥CD,∠B=120°,EF是∠CEB的平分线,FG∥HD,求∠EDH的度数.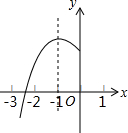 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论: 阅读下列一段文字:已知在平面内两点P1(x1,y1)、P2(x2、y2),其两点间的距离P1P2=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
阅读下列一段文字:已知在平面内两点P1(x1,y1)、P2(x2、y2),其两点间的距离P1P2=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$ 如图所示,∠AOB=45°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD=3$\sqrt{2}$.
如图所示,∠AOB=45°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD=3$\sqrt{2}$.